题目内容
13.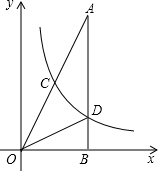 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.(1)求直线AO的解析式;
(2)求反比例函数解析式;
(3)求点C的坐标.
分析 (1)首先根据题意确定A点坐标,然后设直线AO的解析式为y=kx,再把A点坐标代入可得k的值,进而可得函数解析式;
(2)根据△BOD的面积S△BOD=4可得D点坐标,再把D点坐标代入y=$\frac{k}{x}$可得k的值,进而可得函数解析式;
(3)点C是正比例函数和反比例函数的交点,联立两个函数解析式,然后再解可得C点坐标.
解答 解:(1)∵OB=4,AB=8,∠ABO=90°,
∴A点坐标为(4,8),
设直线AO的解析式为y=kx,
则4k=8,解得k=2,
即直线AO的解析式为y=2x;
(2)∵OB=4,S△BOD=4,∠ABO=90°,
∴D点坐标为(4,2),
点D(4,2)代入y=$\frac{k}{x}$,
则2=$\frac{k}{4}$,解得k=8,
∴反比例函数解析式为y=$\frac{8}{x}$;
(3)直线y=2x与反比例函数y=$\frac{8}{x}$构成方程组为$\left\{\begin{array}{l}{y=2x}\\{y=\frac{8}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-4}\end{array}\right.$(舍去),
∴C点坐标为(2,4).
点评 此题主要考查了待定系数法求正比例和反比例函数解析式,以及两函数图象交点问题,关键是掌握凡是函数图象经过的点必能满足解析式.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | a3•a4=a12 | B. | (a3)4=a12 | C. | (a2b)3=a5b3 | D. | a3÷a4=a |
1.下列计算正确的是( )
| A. | x3•x3=2x3 | B. | 4${\;}^{-2}=\frac{1}{16}$ | C. | $\sqrt{9}=±3$ | D. | (x3)2=x5 |
8. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①abc<0;②b=-2a;③b2+4ac>0;④4a+2b+c<0.
其中结论正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc<0;②b=-2a;③b2+4ac>0;④4a+2b+c<0.
其中结论正确的是( )
| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ②③④ |
2.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a6÷a3=a2 | C. | 4x2-3x2=1 | D. | (-2a2)3=-8a6 |
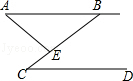 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为73°.
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为73°.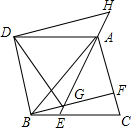 如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH. 如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.
如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.