题目内容
15.在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.

分析 (1)结论:△BCE是等腰三角形,根据平行四边形的性质以及已知条件,只要证明∠CBE=∠BEC即可.
(2)先证明四边形ABCD是矩形,然后分别在RT△ECD,和RT△ABE中利用勾股定理即可解决问题.
解答 (1)如图1中,结论:△BCE是等腰三角形.
证明:∵四边形ABCD是平行四边形,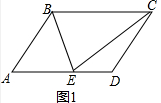
∴BC∥AD,
∴∠CBE=∠AEB,
∵BE平分∠AEC,
∴∠AEB=∠BEC,
∴∠CBE=∠BEC,
∴CB=CE,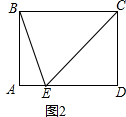
∴△CBE是等腰三角形.
(2)解:如图2中,∵四边形ABCD是平行四边形,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠D=90°,BC=AD=5,
在RT△ECD中,∵∠D=90°,ED=AD-AE=4,EC=BC=5,
∴AB=CD=$\sqrt{E{C}^{2}-{DE}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
在RT△AEB中,∵∠A=90°AB=3.AE=1,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
点评 本题考查平行四边形的性质、矩形的判定和性质、勾股定理、等腰三角形的判定等知识,解题的关键是这些知识的灵活运用,属于中考常考题型.

练习册系列答案
相关题目
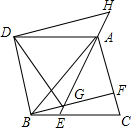 如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.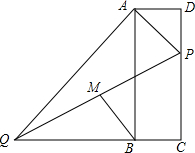 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点. 如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.
如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.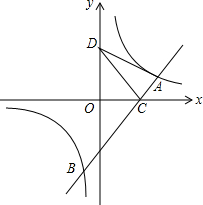 如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC.
如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC. 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.