题目内容
1.计算:($\frac{4}{{x}^{2}{-y}^{2}}$+$\frac{x+y}{{xy}^{2}{-x}^{2}y}$)÷$\frac{{x}^{2}+xy-{2y}^{2}}{{x}^{2}y+2{xy}^{2}}$.分析 根据分式的运算法则即可求出答案.
解答 解:原式=[$\frac{4}{(x+y)(x-y)}$+$\frac{x+y}{xy(y-x)}$]×$\frac{xy(x+2y)}{(x-y)(x+2y)}$
=[$\frac{4}{(x+y)(x-y)}$+$\frac{x+y}{xy(y-x)}$]×$\frac{xy}{x-y}$
=$\frac{4xy}{(x+y)(x-y)^{2}}$-$\frac{x+y}{(x-y)^{2}}$
=$\frac{4xy-(x+y)^{2}}{(x+y)(x-y)^{2}}$
=$\frac{4xy-{x}^{2}-2xy-{y}^{2}}{(x+y)(x-y)^{2}}$
=$\frac{-({x}^{2}-2xy+{y}^{2})}{(x+y)(x-y)^{2}}$
=$\frac{-(x-y)^{2}}{(x+y)(x-y)^{2}}$
=-$\frac{1}{x+y}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
13.实数a,b,c满足2a=5,2b=10,2c=80,则代数式2006a-3344b+1338c的值为( )
| A. | 2007 | B. | 2008 | C. | 2009 | D. | 2010 |
11.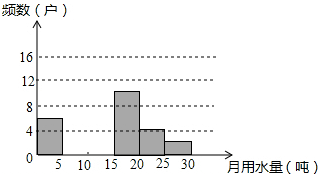 八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
请解答以下问题:
(1)频数分布表中a=12,把频数分布直方图补充完整;
(2)求该居委会用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该居委会有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
 八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | a | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | 0.08 |
| 25<x≤30 | 2 | 0.04 |
(1)频数分布表中a=12,把频数分布直方图补充完整;
(2)求该居委会用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该居委会有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
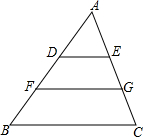 如图,已知△ADE∽△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,其中BC=12cm,求线段DE和FG的长度.
如图,已知△ADE∽△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,其中BC=12cm,求线段DE和FG的长度.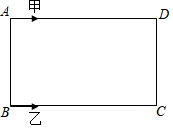 如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.
如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.