题目内容
 如图,平行四边形ABCD的对角线AC,BD相交于点O,AE=EB.求证:OE∥BC.
如图,平行四边形ABCD的对角线AC,BD相交于点O,AE=EB.求证:OE∥BC.考点:三角形中位线定理,平行四边形的性质
专题:证明题
分析:根据平行四边形的对角线互相平分可得AO=CO,然后判断出OE是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半证明.
解答:证明:∵四边形ABCD是平行四边形,
∴AO=CO,
∵AE=EB,
∴OE是△ABC的中位线,
∴OE∥BC.
∴AO=CO,
∵AE=EB,
∴OE是△ABC的中位线,
∴OE∥BC.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的性质,熟记性质与定理是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
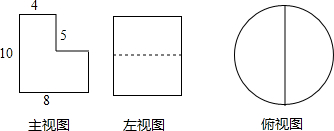 一个几何体的三视图如图所示,你能画出这个几何体吗?并求出它的表面积和体积.
一个几何体的三视图如图所示,你能画出这个几何体吗?并求出它的表面积和体积. 如图,数轴上线段AB的中点表示的数是
如图,数轴上线段AB的中点表示的数是