题目内容
4.分解因式x2+ax+b,甲看错了a的值,分解的结果为(x+6)(x-1),乙看错了b的值,分解结果为(x-2)(x+1),那么x2+ax+b分解因式的正确结果为( )| A. | (x-2)(x+3) | B. | (x+2)(x-3) | C. | (x-2)(x-3) | D. | (x+2)(x+3) |
分析 利用乘法和因式分解的关系,根据甲的分解结果确定b的值,根据乙的分解结果确定a的值,然后分解多项式x2+ax+b.
解答 解:因为(x+6)(x-1)=x2+5x-6,(x-2)(x+1)=x2-x-2,
由于甲看错了a的值没有看错b的值,所以b=6,
乙看错了b的值而没有看错a的值,所以a=-1,
所以多项式x2+ax+b为x2-x+6=(x-3)(x+2)
故选B.
点评 本题考查了多项式乘法和因式分解的关系及因式分解的十字相乘法.解决本题的关键是利用乘法和因式分解的关系确定多项式中a、b的值.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
14.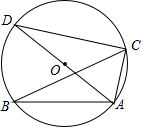 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )
 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )| A. | 25° | B. | 60° | C. | 65° | D. | 75° |
15.下列运算正确的是( )
| A. | (-a)3÷(-a)=a2 | B. | (a2)3=a5 | C. | a2•a3=a6 | D. | a3+a2=a5 |
9.下列语句是命题的是( )
(1)两点之间,线段最短;(2)请画出两条互相平行的直线;
(3)过直线外一点作已知直线的垂线;(4)如果两个角的和是90度,那么这两个角互余.
(1)两点之间,线段最短;(2)请画出两条互相平行的直线;
(3)过直线外一点作已知直线的垂线;(4)如果两个角的和是90度,那么这两个角互余.
| A. | (2)(3) | B. | (3)(4) | C. | (1)(2) | D. | (1)(4) |
14.下列定理中,没有逆定理的是( )
| A. | 全等三角形的对应角相等 | B. | 全等三角形的对应边相等 | ||
| C. | 等腰三角形两底角相等 | D. | a2>b2,则|a|>|b| |
 已知:如图,在△ABC中,AB=AC,点D、E、F分别在边BC、AC、AB上,且有BF=CD,BD=CE.
已知:如图,在△ABC中,AB=AC,点D、E、F分别在边BC、AC、AB上,且有BF=CD,BD=CE.