题目内容
16. 已知:如图,在△ABC中,AB=AC,点D、E、F分别在边BC、AC、AB上,且有BF=CD,BD=CE.
已知:如图,在△ABC中,AB=AC,点D、E、F分别在边BC、AC、AB上,且有BF=CD,BD=CE.(1)求证:△BDF≌△CED;
(2)若设∠FDE=α,则用α表示∠A.
分析 首先证明∠B=∠C,然后再利用SAS定理判定△BDF≌△CED即可,再利用全等三角形的性质解答即可.
解答 证明:(1)∵AB=AC,
∴∠B=∠C,
在△BDF与△CED中,
$\left\{\begin{array}{l}{BF=CD}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$,
∴△BDF≌△CED;
(2)∵△BDF≌△CED,
∴∠BFD=∠CDE,
∵∠FDE+∠CDE=∠B+∠BFD,
∴∠B=∠FDE=α,
∴∠A=180°-2∠B=180°-2α.
点评 此题主要考查了三角形全等的判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.分解因式x2+ax+b,甲看错了a的值,分解的结果为(x+6)(x-1),乙看错了b的值,分解结果为(x-2)(x+1),那么x2+ax+b分解因式的正确结果为( )
| A. | (x-2)(x+3) | B. | (x+2)(x-3) | C. | (x-2)(x-3) | D. | (x+2)(x+3) |
1.某市2016年的地方公共财政收入用四舍五入取近似值后为21.39亿元,则这个数值精确到( )
| A. | 百分位 | B. | 亿位 | C. | 千万位 | D. | 百万位 |
 如图,二次函数y1=ax2+bx+c与反比例函数y2=$\frac{k}{x}$的图象交于A(-1.5,p),B(1,q),C(2.5,r)三点,则当y1<y2时,x的取值范围是-1.5<x<0或1<x<2.5.
如图,二次函数y1=ax2+bx+c与反比例函数y2=$\frac{k}{x}$的图象交于A(-1.5,p),B(1,q),C(2.5,r)三点,则当y1<y2时,x的取值范围是-1.5<x<0或1<x<2.5. 请你在数轴上画出表示$\sqrt{2}$的点(保留作图痕迹)
请你在数轴上画出表示$\sqrt{2}$的点(保留作图痕迹)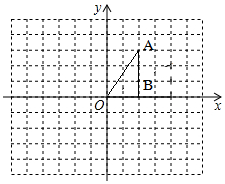 如图,点A的坐标为(2,3),点B的坐标为(2,0),作如下操作;
如图,点A的坐标为(2,3),点B的坐标为(2,0),作如下操作;