题目内容
14．
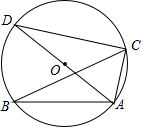如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=25°，则∠CAD的度数是（ ）| A． | 25° | B． | 60° | C． | 65° | D． | 75° |
分析 首先连接CD，由AD是⊙O的直径，根据直径所对的圆周角是直角，可求得∠ACD=90°，又由圆周角定理，可得∠D=∠ABC=25°，继而求得答案．
解答 解：连接CD，
∵AD是⊙O的直径，
∴∠ACD=90°，
∵∠D=∠ABC=25°，
∴∠CAD=90°-∠D=65°．
故选：C．
点评 此题考查了圆周角定理、直角三角形的性质．熟练掌握圆周角定理是解此题的关键．
练习册系列答案
相关题目
2．下列利用等式的性质，错误的是（ ）
| A． | 由a=b，得到1-a=1-b | B． | 由$\frac{a}{2}$=$\frac{b}{2}$，得到a=b | ||
| C． | 由a=b，得到ac=bc | D． | 由ac=bc，得到a=b |
如图，二次函数y1=ax2+bx+c与反比例函数y2=$\frac{k}{x}$的图象交于A（-1.5，p），B（1，q），C（2.5，r）三点，则当y1＜y2时，x的取值范围是-1.5＜x＜0或1＜x＜2.5．
4．分解因式x2+ax+b，甲看错了a的值，分解的结果为（x+6）（x-1），乙看错了b的值，分解结果为（x-2）（x+1），那么x2+ax+b分解因式的正确结果为（ ）
| A． | （x-2）（x+3） | B． | （x+2）（x-3） | C． | （x-2）（x-3） | D． | （x+2）（x+3） |