题目内容
8.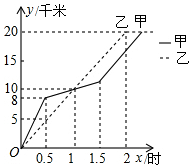 在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:
在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;
②出发后1小时,两人行程均为10km;
③出发后1.5小时,甲的行程比乙多3km;
④甲比乙先到达终点.
其中正确的有3个.
分析 根据题目所给的图示可得,两人在1小时时相遇,行程均为10km,出发0.5小时之内,甲的速度大于乙的速度,0.5至1小时之间,乙的速度大于甲的速度,出发1.5小时之后,乙的路程为15千米,甲的路程为12千米,再利用函数图象横坐标,得出甲先到达终点.
解答 解:在两人出发后0.5小时之前,甲的速度小于乙的速度,0.5小时到1小时之间,甲的速度大于乙的速度,故①错误;
由图可得,两人在1小时时相遇,行程均为10km,故②正确;
甲的图象的解析式为y=10x,乙AB段图象的解析式为y=4x+6,因此出发1.5小时后,甲的路程为15千米,乙的路程为12千米,甲的行程比乙多3千米,故③正确;
甲到达终点所用的时间较少,因此甲比乙先到达终点,故④正确.
故答案为3.
点评 本题考查了一次函数的应用,行程问题的数量关系速度=路程后÷时间的运用,解答时理解函数的图象的含义是关键.

练习册系列答案
相关题目
13.下列说法不正确的是( )
| A. | 平行四边形的对边平行且相等 | B. | 平行四边形对角线互相平分 | ||
| C. | 平行四边形是轴对称图形 | D. | 平行四边形是中心对称图形 |
20.下列各命题不成立的是( )
| A. | 平行四边形的对边平行且相等 | |
| B. | 依次连结正方形各边中点所得的四边形是正方形 | |
| C. | 对角线互相平分且相等的四边形是矩形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
17.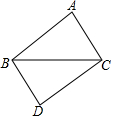 如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )
如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )
 如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )
如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )| A. | ∠A=∠D | B. | AC=BC | C. | ∠ACB=∠DBC | D. | ∠ABC=∠DCB |
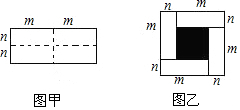 已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
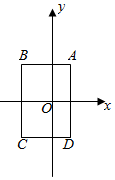 如图所示,在平面直角坐标系中,已知点A (1,2),B (-2,2),C (-2,-2),D(1,-2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→D→C→B→A…的顺序紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
如图所示,在平面直角坐标系中,已知点A (1,2),B (-2,2),C (-2,-2),D(1,-2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→D→C→B→A…的顺序紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )