题目内容
2.已知:a+$\frac{1}{a}$=m.(1)当m=$\sqrt{5}$,求a2+$\frac{1}{{a}^{2}}$的值;
(2)问m能否等于$\sqrt{3}$,说明理由.
分析 (1)将a+$\frac{1}{a}$=m两边平方即可得出a2+$\frac{1}{{a}^{2}}$的值;
(2)令m=$\sqrt{3}$,计算一下即可得出结论.
解答 解:(1)∵a+$\frac{1}{a}$=m,
∴(a+$\frac{1}{a}$)2=m2,
∴a2+$\frac{1}{{a}^{2}}$=m2-2,
∵m=$\sqrt{5}$,
∴a2+$\frac{1}{{a}^{2}}$=m2-2=5-2=3;
(2)令m=$\sqrt{3}$,
∴a2+$\frac{1}{{a}^{2}}$=m2-2=3-2=1;
∴a4-a2+1=0,
∵△=1-4=-3<0,
∴方程无实数根,
∴m不能否等于$\sqrt{3}$.
点评 本题考查了分式的化简求值以及完全平方公式,解这类题的关键是熟记完全平方公式,特别注意完全平方公式的逆用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目

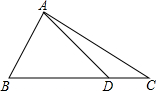 如图,在△ABC中,D是边BC上一点,BD=3DC,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示).
如图,在△ABC中,D是边BC上一点,BD=3DC,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示).