��Ŀ����
14����ͼ��һֻ��ţA��ԭ����������Ḻ�����˶���ͬʱ����һֻ��ţBҲ��ԭ������������������˶���3$\sqrt{2}$�������ţ���15����λ���ȣ���֪��ţA��B���ٶȱ���1��4�����ٶȵ�λ����λ����/�룩��1�����������ţ�˶����ٶȣ����������ϣ�ͼ1�����A��B��ԭ������˶�3$\sqrt{2}$��ʱ��λ�ã�
��2������ţA��B�ӣ�1���е�λ��ͬʱ�����Ḻ�����˶�������ʱ��ԭ��ǡ�ô�����ֻ��ţ�����м䣿
��3������ţA��B�ӣ�1���е�λ��ͬʱ�����Ḻ�����˶�ʱ����һ��ţCҲͬʱ����ţB��λ�ó�������ţA�˶�����������ţA��������������ţB�˶���������ţB����������������ţA�˶������������ֱ��B��Aʱ����ţC����ֹͣ�˶�������ţCһֱ��2$\sqrt{5}$��λ����/����ٶ������˶�����ô��ţC�ӿ�ʼ�˶���ֹͣ�˶�����ʻ��·���Ƕ��ٸ���λ���ȣ�

���� ��1������ţA���ٶ�Ϊx��λ����/�룬��ţB���ٶ�Ϊ4x��λ����/�룬��������ţ���15����λ�г�������⼴�ɣ�
��2�������෴���Ķ��壬��ţA��B��ԭ��ľ�����ȣ��ֱ��ʾ����ţA��B����Ӧ�����ľ���ֵ��Ȼ���г�������⼴�ɣ�
��3����y�����ţB����ţA��������ţB����ţA��·�̶�15�г����̣����õ�ʱ�䣬�ٸ���·��=�ٶȡ�ʱ����м��㼴�ɵý⣮
��� �⣺��1������ţA���ٶ�Ϊx��λ����/�룬��ţB���ٶ�Ϊ4x��λ����/�룬
�������⣬3$\sqrt{2}$��x+4x��=15��
��ã�x=$\frac{\sqrt{2}}{2}$��
������ţA���ٶ�Ϊ$\frac{\sqrt{2}}{2}$��λ����/�룬��ţB���ٶ�Ϊ2$\sqrt{2}$��λ����/�룬
3$\sqrt{2}$��ʱ����ţA��λ����-$\frac{3}{2}\sqrt{2}$����ţB��λ����6$\sqrt{2}$��
��ͼ1�ϱ�ע���£�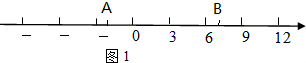
��2����x��ʱԭ��ǡ�ô���������ţ�����м䣬
������ã�6$\sqrt{2}$-4x=$\frac{3}{2}\sqrt{2}$+x��
��ã�x=$\frac{9}{10}\sqrt{2}$��
��3����y�����ţB����ţA��
������ã�2$\sqrt{2}$y-$\frac{\sqrt{2}}{2}$y=15��
��ã�y=5$\sqrt{2}$��
5$\sqrt{2}$��2$\sqrt{5}$=10$\sqrt{10}$��
��C�ӿ�ʼ�˶���ֹͣ�˶�����ʻ��·����10$\sqrt{10}$����λ���ȣ�
���� ���⿼����һԪһ�η��̵�Ӧ�ã�����ؼ���Ҫ������Ŀ����˼��������Ŀ�������������ҳ����ʵĵ�����ϵ�г����̣�����⣮

| A�� | ƽ���ı��� | B�� | ���� | C�� | ���� | D�� | ������ |
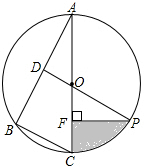 ��ͼ����֪��O�ǡ�ABC�����Բ��AC��ֱ������A=30�㣬BC=2����D��AB���е㣬����DO���ӳ�����O�ڵ�P������P��PF��AC�ڵ�F��
��ͼ����֪��O�ǡ�ABC�����Բ��AC��ֱ������A=30�㣬BC=2����D��AB���е㣬����DO���ӳ�����O�ڵ�P������P��PF��AC�ڵ�F��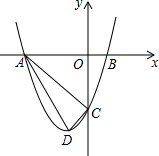 ���κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��-3��0����B��1��0�����㣬��y�ύ�ڵ�C��0��-3m��������m��0��������ΪD��
���κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��-3��0����B��1��0�����㣬��y�ύ�ڵ�C��0��-3m��������m��0��������ΪD��