题目内容
11.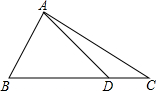 如图,在△ABC中,D是边BC上一点,BD=3DC,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示).
如图,在△ABC中,D是边BC上一点,BD=3DC,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示).
分析 由在△ABC中,D是边BC上一点,BD=3DC,即可表示出$\overrightarrow{BD}$,然后由三角形法则,求得$\overrightarrow{AD}$.
解答 解:∵在△ABC中,D是边BC上一点,BD=3DC,
∴$\overrightarrow{BD}$=$\frac{3}{4}$$\overrightarrow{BC}$=$\frac{3}{4}$$\overrightarrow{b}$,
∴$\overrightarrow{AD}$=$\overrightarrow{BD}$-$\overrightarrow{BA}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$.
故答案为:$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用.

练习册系列答案
相关题目
1.已知x2-3x+1=0,则x4+$\frac{1}{x^{4}}$的值为( )
| A. | 7 | B. | 47 | C. | 9 | D. | 49 |
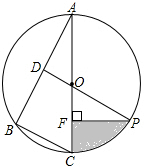 如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.
如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.