题目内容
18.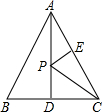 如图,在边长为2的等边△ABC中,AD是BC边上的高线,点E是AC中点,点P是AD上一动点,则PC+PE的最小值是$\sqrt{3}$.
如图,在边长为2的等边△ABC中,AD是BC边上的高线,点E是AC中点,点P是AD上一动点,则PC+PE的最小值是$\sqrt{3}$.
分析 连接BE,则BE的长度即为PE与PC和的最小值.
解答 解:如连接BE,与AD交于点P,此时PE+PC最小,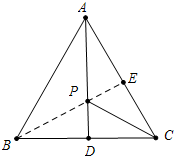
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是一个边长为2cm的正三角形,点E是边AC的中点,
∴∠BEC=90°,CE=1cm,
∴BE=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴PE+PC的最小值是$\sqrt{3}$.
故答案为$\sqrt{3}$,
点评 本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
3.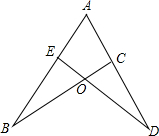 如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是( )
如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是( )
 如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是( )
如图,若已知AE=AC,用“SAS”说明△ABC≌△ADE,还需要的一个条件是( )| A. | BC=DE | B. | AB=AD | C. | BO=DO | D. | EO=CO |
 如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,点B,交y轴于点E,其中B点的坐标为(3,0),OB=3OA,连接AE,tan∠EAO=3,直线y=-2x-2交x轴于点C,交y轴于点D.
如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,点B,交y轴于点E,其中B点的坐标为(3,0),OB=3OA,连接AE,tan∠EAO=3,直线y=-2x-2交x轴于点C,交y轴于点D.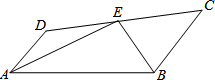 如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°.设AD=x,BC=y,且(x-3)2+|y-4|=0,AB的长度是( )
如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°.设AD=x,BC=y,且(x-3)2+|y-4|=0,AB的长度是( )