题目内容
8. 如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,点B,交y轴于点E,其中B点的坐标为(3,0),OB=3OA,连接AE,tan∠EAO=3,直线y=-2x-2交x轴于点C,交y轴于点D.
如图,抛物线y=ax2+bx+c(a≠0)交x轴于点A,点B,交y轴于点E,其中B点的坐标为(3,0),OB=3OA,连接AE,tan∠EAO=3,直线y=-2x-2交x轴于点C,交y轴于点D.(1)求抛物线的函数表达式;
(2)若M是抛物线上不同于点A,点B的另一点,Q是抛物线对称轴上的点,求以A、B、M、Q为顶点的四边形为平行四边形时点M的坐标;
(3)若P(x,y)(x>0)是抛物线上一动点,求使△PCD的面积最小时点P的坐标及△PCD面积的最小值.
分析 (1)根据OB与OA的关系,可得A点坐标,根据三角函数,可得C点坐标,根据待定系数法,可得答案;
(2)根据平行四边形的对边相等,可得m的值,根据自变量与函数值的对应关系,可得答案;
(3)根据平行于CD且与抛物线相切,可得P点坐标,根据面积的和差,可得答案.
解答 解:(1)由B点的坐标为(3,0),OB=3OA,得
A(1,0).
由tan∠EAO=$\frac{EO}{AO}$=3,得
EO=3AO=3,即E(0,3).
将A、B、E代入函数解析式,得
$\left\{\begin{array}{l}{9a+3b+c=0}\\{a+b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$,
抛物线的解析式为y=x2-4x+3;
(2)如图1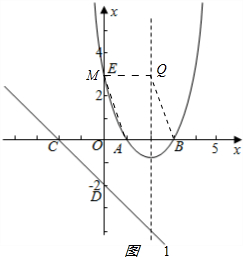 ,
,
设M(m,x2-4x+3),MQ=2-m.AB=3-1=2.
由四边形ABQE是平行四边形,得
EQ=AB,即2-m=2.
解得m=0,
当m=0时,y=3,即M(0,3);
如图2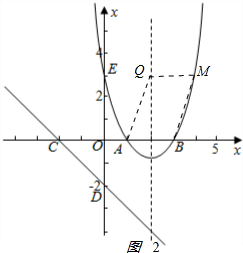 ,
,
设M(m,x2-4x+3),MQ=m-2.AB=3-1=2.
由四边形ABQE是平行四边形,得
EQ=AB,即m-2=2.
解得m=4,
当m=4时,y=3,即M(4,3);
综上所述:以A、B、M、Q为顶点的四边形为平行四边形时点M的坐标(0,3)或(4,3);
(3)如图3 ,
,
CD的解析式为y=-x-2,设平行CD与抛物线相切于P点的直线为y=-x+b,
联立过P点的切线与抛物线,得
$\left\{\begin{array}{l}{y=-x+b}\\{y={x}^{2}-4x+3}\end{array}\right.$,
x2-3x+3-b=0.
△=b2-4ac=(-3)2-4×(3-b)=0.
解得b=$\frac{3}{4}$.
当b=$\frac{3}{4}$时,x2-3x+$\frac{9}{4}$=0,
解得x=$\frac{3}{2}$,y=-$\frac{3}{2}$+$\frac{3}{4}$=-$\frac{3}{4}$,
即P点坐标为($\frac{3}{2}$,-$\frac{3}{4}$).
设CP的解析式为y=kx+b,将C、P点坐标代入函数解析式,
$\left\{\begin{array}{l}{\frac{3}{2}k+b=-\frac{3}{4}}\\{-2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{14}}\\{b=-\frac{3}{7}}\end{array}\right.$,
CP的解析式为y=-$\frac{3}{14}$x-$\frac{3}{7}$,
当x=0时,y=-$\frac{3}{7}$,即F(0,-$\frac{3}{7}$).
CF=-$\frac{3}{7}$-(-2)=$\frac{11}{7}$.
S△PCD最小=$\frac{1}{2}$PD(xP-xC)=$\frac{1}{2}$×$\frac{11}{7}$×[$\frac{3}{2}$-(-2)]=$\frac{11}{4}$.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用平行四边形的对边相等得出关于m的方程是解题关键,要分类讨论,以防遗漏;利用平行于CD且与抛物线相切得出P点坐标是解题关键,利用面积的和差是求面积的关键.

 如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )
如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
 如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.
如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.
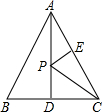 如图,在边长为2的等边△ABC中,AD是BC边上的高线,点E是AC中点,点P是AD上一动点,则PC+PE的最小值是$\sqrt{3}$.
如图,在边长为2的等边△ABC中,AD是BC边上的高线,点E是AC中点,点P是AD上一动点,则PC+PE的最小值是$\sqrt{3}$.