题目内容
3. 将矩形ABCD折叠,点A与对角线BD上的点G重合,折痕BE交AD于点E,点C与对角线上的点H重合,折痕DF交BC于点F.
将矩形ABCD折叠,点A与对角线BD上的点G重合,折痕BE交AD于点E,点C与对角线上的点H重合,折痕DF交BC于点F.(1)求证:四边形BEDF是平行四边形;
(2)若AB=6,AD=8,求EH的长.
分析 (1)利用矩形性质得出∠ABE=∠CDF,∠EBD=∠FDB,进而得出△ABE≌△CDF,即可得出EB∥DF,EB=DF,即可得出答案;
(2)根据勾股定理即可得到结论.
解答 (1)证明:∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,∠A=∠C.
∴∠ABD=∠CDB,
由翻折知,∠ABE=∠EBD=$\frac{1}{2}$∠ABD,∠CDF=∠FDB=$\frac{1}{2}$∠CDB,
∴∠ABE=∠CDF,∠EBD=∠FDB,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{AB=CD}\\{∠A=∠C}\end{array}\right.$,
∴△ABE≌△CDF(ASA),
∴EB=DF,
∵∠EBD=∠FDB,
∴EB∥DF,
∴四边形EBDF为平行四边形.
(2)∵AB=6,AD=8,
∴BD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴设EG=x,则AE=x,DE=(8-x),AB=BG=6,则DG=10-6=4,
在Rt△DEG中,DG2+EG2=DE2,
∴42+x2=(8-x)2,
解得:x=3,
∴EG=3,
∵DH=BG=6,
∴HG=2,
∴EH=$\sqrt{E{G}^{2}+H{G}^{2}}$=$\sqrt{13}$.
点评 此题主要考查了矩形的性质以及全等三角形的判定与性质和平行四边形的判定以及勾股定理等知识,根据已知得出△ABE≌△CDF是解题关键.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
11.函数y=ax2的图象与a无关的是( )
| A. | 开口方向 | B. | 开口大小 | C. | 最高点的坐标 | D. | 对称轴 |
15.在一个三角形的外角中,钝角至少有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |

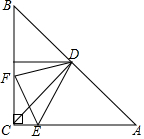 已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.
已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.