题目内容
14.如图,A、B、C、D是数轴上四点,且A:-13,B:-10,C:14,D:20.(1)线段AB以4个单位/秒的速度向右运动,线段CD以2个单位/秒的速度向左运动,几秒后,B、C相距10个单位长度;
(2)P为数轴上一动点,当PA+PB+PC+PD=80时,求P点对应的数;
(3)在(1)的条件下,当点B运动到线段CD上,且P在线段AB上的一点时,问是否存在等式BD-PA=3PC成立?若存在,求PD的长,若不存在,请说明理由.

分析 (1)设t秒后,B、C相距10个单位长度,根据各自的速度表示出点B和C所到位置表示的数,要分两种情况:①点B在点C的左侧时,②点B在点C的右侧时,列式计算;
(2)先设点P表示的数为a,分五种情况讨论,根据两点的距离公式代入PA+PB+PC+PD=80中列式,解方程即可;
(3)先根据(1)中的速度和时间表示出A、B、C、D四点所表示的数,按向左减,向右加的原则,再设分两种情况讨论:①当点P在C的右侧时,如图6,②当点P在C的左侧时,如图7,设PA=x,则P表示的数为:-13+4t+x,根据BD-PA=3PC列式计算即可.
解答  解:(1)设t秒后,B、C相距10个单位长度,
解:(1)设t秒后,B、C相距10个单位长度,
t秒后,点B由-10运动到-10+4t,
点C由14运动到14-2t,
则-10+4t-(14-2t)=10或14-2t-(-10+4t)=10,
解得t=$\frac{17}{3}$或$\frac{7}{3}$,
答:$\frac{17}{3}$秒或$\frac{7}{3}$秒后,B、C相距10个单位长度;
(2)设点P表示的数为a,
分五种情况:
①当P在点D的右侧时,如图1,
由题意得:a+13+a+10+a-14+a-20=80,
a=$\frac{91}{4}$,
②当P在C、D之间时,如图2,
由题意得:a+13+a+10+a-14+20-a=80,
a=$\frac{51}{2}$(不符合题意,舍),
③当P在B、C之间时,如图3,
由题意得:a+13+a+10+14-a+20-a=80
此方程无解,
④当P在A、B之间时,如图4,
由题意得:a+13-10-a+14-a+20-a=80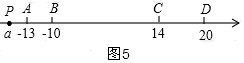
a=-$\frac{43}{2}$(不符合题意,舍),
⑤当P在A的左侧时,如图5,
由题意得:-13-a-10-a+14-a+20-a=80
a=-$\frac{69}{4}$
综上所述,P点对应的数是$\frac{91}{4}$或-$\frac{69}{4}$;
(3)存在,
t秒后,A表示的数为:-13+4t,
B表示的数为:-10+4t,
C表示的数为:14-2t,
D表示的数为:20-2t,
设PA=x,则P表示的数为:-13+4t+x,
①当点P在C的右侧时,如图6,
∵BD-PA=3PC,
∴20-2t-(-10+4t)-x=3(-13+4t+x-14+2t),
x=$\frac{111-24t}{4}$,
则P表示的数为:-13+4t+x=-13+4t+$\frac{111-24t}{4}$=-2t+$\frac{69}{4}$,
∴PD=20-2t+2t-$\frac{69}{4}$=20-17.25=2.75;
②当点P在C的左侧时,如图7,
同理得:20-2t-(-10+4t)-x=3(14-2t+13-4t-x),
x=$\frac{-12t+51}{2}$,
则P表示的数为:-13+4t+x=-13+4t+$\frac{-12t+51}{2}$=-2t+12.5,
∴PD=20-2t-(-2t+12.5)=7.5,
综上所述,PD的长为2.75或7.5.
点评 本题考查了数轴,涉及的知识点有:非负数的性质、数轴上两点的距离、路程问题,综合性较强,有一定的难度.

| A. | (4,4) | B. | (3,-1) | C. | (-3,-1) | D. | (-$\frac{1}{2}$,-$\frac{7}{4}$) |
 如图,在Rt△ABC中,∠ABC=90°,以AC为斜边向外作等腰Rt△ACD,连接BD.
如图,在Rt△ABC中,∠ABC=90°,以AC为斜边向外作等腰Rt△ACD,连接BD.
 如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.
如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.
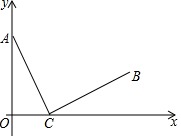 已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.
已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC. 将矩形ABCD折叠,点A与对角线BD上的点G重合,折痕BE交AD于点E,点C与对角线上的点H重合,折痕DF交BC于点F.
将矩形ABCD折叠,点A与对角线BD上的点G重合,折痕BE交AD于点E,点C与对角线上的点H重合,折痕DF交BC于点F.