题目内容
18.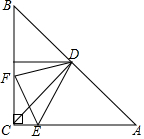 已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.
已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.(1)求证:CD⊥AB;
(2)求证:CE+EF=BF.
分析 (1)根据等腰直角三角形的性质即可得到结论;
(2)过D作DG⊥DE交AB于G,根据等腰直角三角形的性质得到CD=BD,∠ACD=∠B=45°,通过全等三角形得到BG=CE,DG=DE,EF=GF,根据得到结论.
解答 解:(1)∵△ACB为等腰直角三角形,
∴AC=BC,
∵D为BA的中点,
∴CD⊥AB;
(2)过D作DG⊥DE交AB于G,
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=BD,∠ACD=∠B=45°,
∵∠EDG=∠CDB=90°,
∴∠CDE=∠BDG,
在△CDE与△BDG中,$\left\{\begin{array}{l}{∠ECD=∠B}\\{CD=BD}\\{∠CDE=∠BDG}\end{array}\right.$,
∴△CDE≌△BDG,
∴BG=CE,DG=DE,
在△EDF与△GDF中,$\left\{\begin{array}{l}{DE=DG}\\{∠EDF=∠GDF}\\{DF=DF}\end{array}\right.$,
∴△EDF≌△GDF,
∴EF=GF,
∵BF=BG+GF,
∴BF=CE+EF.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.关于抛物线y=ax2和y=-ax2(a≠0),给出下列说法:
①两条抛物线都关于x轴对称;
②两条抛物线都关于原点对称;
③两条抛物线各自关于y轴对称;
④两条抛物线有公共的顶点.
其中正确的说法有( )
①两条抛物线都关于x轴对称;
②两条抛物线都关于原点对称;
③两条抛物线各自关于y轴对称;
④两条抛物线有公共的顶点.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.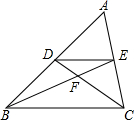 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )| A. | $\frac{DF}{FC}=\frac{AE}{AC}$ | B. | $\frac{AD}{AB}=\frac{EC}{AC}$ | C. | $\frac{AD}{DB}=\frac{DE}{BC}$ | D. | $\frac{DF}{BF}=\frac{EF}{FC}$ |
5.计算2x2-3x2的结果是( )
| A. | 5x2 | B. | -5x2 | C. | x2 | D. | -x2 |
5.下列二次根式中与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
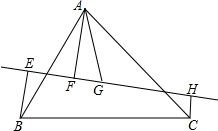 如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF.
如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF. 如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.
如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.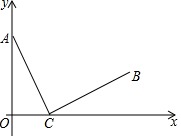 已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.
已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC. 将矩形ABCD折叠,点A与对角线BD上的点G重合,折痕BE交AD于点E,点C与对角线上的点H重合,折痕DF交BC于点F.
将矩形ABCD折叠,点A与对角线BD上的点G重合,折痕BE交AD于点E,点C与对角线上的点H重合,折痕DF交BC于点F.