题目内容
8.在一个不透明的盒子中装有6个白球,若干个黄球,它们除颜色不同外,其余均相同,若从中随机摸出一个球是白球的概率是$\frac{1}{3}$,则黄球的个数为( )| A. | 18 | B. | 12 | C. | 9 | D. | 24 |
分析 首先设黄球的个数为x个,根据题意得:$\frac{6}{6+x}$=$\frac{1}{3}$,解此分式方程即可求得答案.
解答 解:设黄球的个数为x个,
根据题意得:$\frac{6}{6+x}$=$\frac{1}{3}$,
解得:x=12,
经检验:x=12是原分式方程的解;
∴黄球的个数为12.
故选:B.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
18.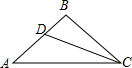 如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
 如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )
如图,在△ABC中,∠A=∠ACB,CD平分∠ACB交AB于点D,∠ADC=150°,则∠B为( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
18. 如图,把△ABC沿AD折叠,使点C落在AB上点E处,那么折痕AD是△ABC的( )
如图,把△ABC沿AD折叠,使点C落在AB上点E处,那么折痕AD是△ABC的( )
 如图,把△ABC沿AD折叠,使点C落在AB上点E处,那么折痕AD是△ABC的( )
如图,把△ABC沿AD折叠,使点C落在AB上点E处,那么折痕AD是△ABC的( )| A. | 角平分线 | B. | 中线 | C. | 高线 | D. | 角平分线 |
15.九台全区7年级学生大约有10200人,10200这个数用科学记数法表示为( )
| A. | 1.02×105 | B. | 1.02×104 | C. | 10.2×103 | D. | 102×102 |

 将矩形ABCD折叠,点A与对角线BD上的点G重合,折痕BE交AD于点E,点C与对角线上的点H重合,折痕DF交BC于点F.
将矩形ABCD折叠,点A与对角线BD上的点G重合,折痕BE交AD于点E,点C与对角线上的点H重合,折痕DF交BC于点F. 如图是一个几何体分别从正面、左面、上面看到的形状图,则与之相对应的几何体是( )
如图是一个几何体分别从正面、左面、上面看到的形状图,则与之相对应的几何体是( )


