题目内容
13.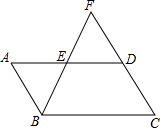 如图,?ABCD中,E为AD的中点,BE、CD相交于点F.
如图,?ABCD中,E为AD的中点,BE、CD相交于点F.(1)求证:AB=DF
(2)若△DEF的面积为S1,△BCF的面积为S2,且S12-S2+4=0,求?ABCD的面积.
分析 (1)根据平行四边形的性质得到AB∥CD,AB=CD,平行线的性质得到∠A=∠EDF,根据全等三角形的性质即可得到结论;
(2)根据全等三角形的性质得到DE=AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,根据相似三角形的性质得到$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{4}$,求得S2=4S1,解方程得到S1=2,求得S2=8,于是得到结论.
解答  (1)证明:∵四边形ABCD为平行四边形,
(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠A=∠EDF,
又∵E为AD中点,
∴AE=DE,
在△ABE和△DFE中$\left\{{\begin{array}{l}{∠A=∠EDF}\\{AE=DE}\\{∠1=∠2}\end{array}}\right.$,
∴△ABE≌△DFE(ASA),
∴AB=DF,
(2)解:∵△ABE≌△DFE,
∴DE=AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∵DE∥BC,
∴△FED∽△FBC
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{4}$,
∴即S2=4S1,
∵S12-S2+4=0,
∴S12-4S1+4=0,∴S1=2,
∴S2=8,
又∵△ABE≌△DFE,
∴?ABCD的面积=S△BCF=8.
点评 本题考查了相似三角形的,平行四边形的性质,全等三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
8.当a=$\sqrt{2}$时,计算分式$\frac{a+3}{a}$•$\frac{6}{{a}^{2}+6a+9}$+$\frac{2a-6}{{a}^{2}-9}$的值是$\sqrt{2}$.
18.快递公司2014年的快递业务量为2亿件,受益于经济的快速增长及电子商务发展等多重因素,快递业务迅猛发展,2016年的快递业务量达到3.92亿件.若设该地区这两年快递业务量的年平均增长率为x,则下列方程正确的是( )
| A. | 2(1-x)2=3.92 | B. | 3.92(1-x)2=2 | C. | 2(1+x)2=3.92 | D. | 3.92(1+x)2=2 |
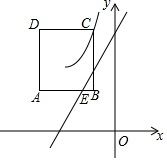 如图,在平面直角坐标系中,边长为2的正方形ABCD位于第二象限,且AB∥x轴,点B在点C的正下方,双曲线y=$\frac{1-2m}{x}$(x<0)经过点C.
如图,在平面直角坐标系中,边长为2的正方形ABCD位于第二象限,且AB∥x轴,点B在点C的正下方,双曲线y=$\frac{1-2m}{x}$(x<0)经过点C.
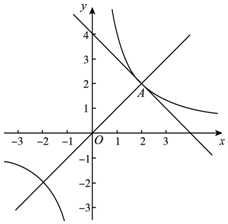 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+4(a≠0)的图象只有一个公共点A(2,2),直线y=mx(m≠0)也过点A.
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+4(a≠0)的图象只有一个公共点A(2,2),直线y=mx(m≠0)也过点A.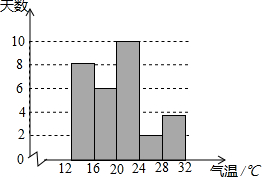 为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.
为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.