题目内容
1.解不等式(组)(1)$\frac{1}{2}$x-1≤$\frac{2}{3}$x-$\frac{1}{2}$,并把它的解集在数轴上表示出来.
(2)$\left\{\begin{array}{l}{2(x-1)>3}\\{x<10-x}\end{array}\right.$,并把它的解集在数轴上表示出来.
(3)$\left\{\begin{array}{l}{9x+5<8x+7}\\{\frac{4}{3}x+2>1-\frac{2}{3}x}\end{array}\right.$并写出其整数解.
(4)$\left\{\begin{array}{l}{3(x-1)<5x+1}\\{\frac{x-1}{2}≥2x-4}\end{array}\right.$,并指出它的所有的非负整数解.
分析 (1)根据解一元一次不等式基本步骤:去分母、移项、合并同类项可得.
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
(3)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集;
(4)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)去分母,得:3x-6≤4x-3,
移项、合并,得:x>-3,
表示在数轴上如下:
(2)解不等式2(x-1)>3,得:x>$\frac{5}{2}$,
解不等式x<10-x,得:x<5,
则不等式组的解集为$\frac{5}{2}$<x<5,
表示在数轴上如下: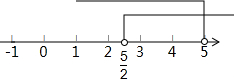
(3)解不等式9x+5<8x+7,得:x<2,
解不等式$\frac{4}{3}$x+2>1-$\frac{2}{3}$x,得:x>-$\frac{1}{2}$,
则不等式组的解集为-$\frac{1}{2}$<x<2,
则其整数解为0、1;
(4)解不等式3(x-1)<5x+1,得:x>-2,
解不等式$\frac{x-1}{2}$≥2x-4,得:x≤$\frac{7}{3}$,
∴不等式组的解集为-2<x≤$\frac{7}{3}$,
则其非负整数解为0、1、2.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
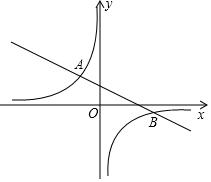 如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
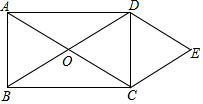 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.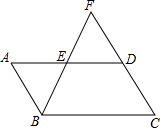 如图,?ABCD中,E为AD的中点,BE、CD相交于点F.
如图,?ABCD中,E为AD的中点,BE、CD相交于点F.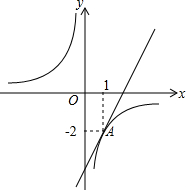 如图,直线y=2x+b与双曲线y=$\frac{k}{x}$(k≠0)只有一个公共点A(1,-2).
如图,直线y=2x+b与双曲线y=$\frac{k}{x}$(k≠0)只有一个公共点A(1,-2).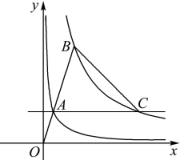 如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.
如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.