题目内容
17.阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如:$\frac{8}{3}$=$\frac{6+2}{3}$=2+$\frac{2}{3}$=2$\frac{2}{3}$.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如:$\frac{x-1}{x+1}$,$\frac{{x}^{2}}{x-1}$这样的分式就是假分式;再如:$\frac{3}{x+1}$,$\frac{2x}{{x}^{2}+1}$这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如:$\frac{x-1}{x+1}$=$\frac{(x+1)-2}{x+1}$=1-$\frac{2}{x+1}$;
再如:$\frac{{x}^{2}}{x-1}$=$\frac{{x}^{2}-1+1}{x-1}$=$\frac{(x+1)(x-1)+1}{x-1}$=x+1+$\frac{1}{x-1}$.
解决下列问题:
(1)分式$\frac{2}{x}$是真分式(填“真分式”或“假分式”);
(2)假分式$\frac{x-1}{x+2}$可化为带分式1-$\frac{3}{x+2}$的形式;
(3)如果分式$\frac{2x-1}{x+1}$的值为整数,那么x的整数值为0,-2,2,-4.
分析 (1)依据定义进行判断即可;
(2)将原式变形为$\frac{x+2-3}{x+2}$的形式,然后再进行变形即可;
(3)首先将原式变形为2-$\frac{3}{x+1}$,然后依据x+1能够被3整数列方程求解即可.
解答 解:(1)分式$\frac{2}{x}$是 真分式;
(2)假分式$\frac{x-1}{x+2}$=1-$\frac{3}{x+2}$;
(3)$\frac{2x-1}{x+1}$=$\frac{2x+2-3}{x+1}$=2-$\frac{3}{x+1}$.
所以当x+1=3或-3或1或-1时,分式的值为整数.
解得x=2或x=-4或x=0或x=-2.
故答案为:(1)真;(2)1-$\frac{3}{x+2}$;(3)0,-2,2,-4.
点评 本题主要考查的是分式的基本性质,熟练掌握分式的基本性质是解题的关键.

练习册系列答案
相关题目
7. 如图,AE⊥BC于E,BF⊥AC于F,CD⊥AB于D,则△ABC中AC边上的高是哪条垂线段( )
如图,AE⊥BC于E,BF⊥AC于F,CD⊥AB于D,则△ABC中AC边上的高是哪条垂线段( )
 如图,AE⊥BC于E,BF⊥AC于F,CD⊥AB于D,则△ABC中AC边上的高是哪条垂线段( )
如图,AE⊥BC于E,BF⊥AC于F,CD⊥AB于D,则△ABC中AC边上的高是哪条垂线段( )| A. | BF | B. | CD | C. | AE | D. | AF |
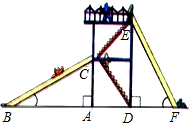 如图,幼儿园的滑梯有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.
如图,幼儿园的滑梯有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.