题目内容
2.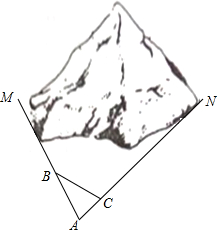 (1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.(2)列方程(组)或不等式(组)解应用题:
2015年的5月20日是第15个中国学生营养日,我市某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如表).
| 信息 1、快餐成分:蛋白质、脂肪、碳水化合物和其他 2、快餐总质量为400克 3、碳水化合物质量是蛋白质质量的4倍 |
分析 (1)先根据相似三角形的判定得出△ABC相似与△AMN,再利用相似三角形的性质解答即可;
(2)设这份快餐含有x克的蛋白质,根据所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%,列出不等式,求解即可.
解答 解:(1)在△ABC与△AMN中,
∠A=∠A,$\frac{AC}{AB}=\frac{30}{54}=\frac{5}{9},\frac{AM}{AN}=\frac{1}{1.8}=\frac{5}{9}$,
∴△ABC∽△AMN,
∴$\frac{AC}{BC}=\frac{AM}{MN}$,即$\frac{30}{45}=\frac{1}{MN}$,
解得:MN=1.5千米,
答:M、N两点之间的直线距离是1.5千米;
(2)设这份快餐含有x克的蛋白质,
根据题意可得:x+4x≤400×70%,
解不等式,得x≤56.
答:这份快餐最多含有56克的蛋白质.
点评 此题考查相似三角形和一元一次不等式的应用,关键是根据相似三角形的判定和性质解答问题,读懂题意,找出题目中的数量关系,列出不等式,本题的数量关系是所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%.

练习册系列答案
相关题目
10.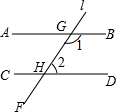 如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
 如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 75° |
14.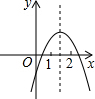 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )
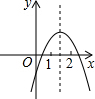 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.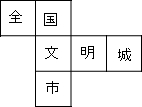 在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
 在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )| A. | 全 | B. | 明 | C. | 城 | D. | 国 |
12.下列几何体中,俯视图是矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
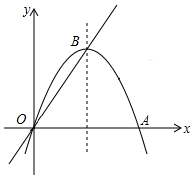 如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.
如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.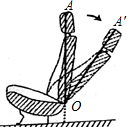 如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O旋转35°到OA′处,求调整后点A′比调整前点A的高度降低了多少厘米(结果取整数)?
如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O旋转35°到OA′处,求调整后点A′比调整前点A的高度降低了多少厘米(结果取整数)?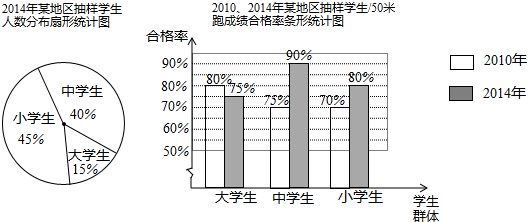
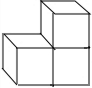 用3个完全相同的小正方体组成如图所示的几何体,则它的俯视图是( )
用3个完全相同的小正方体组成如图所示的几何体,则它的俯视图是( )