题目内容
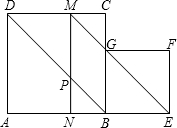 如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.
如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.(1)证明:四边形MPBG是平行四边形;
(2)设BE=x,四边形MNBG的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)如果按题设作出的四边形BGMP是菱形,求BE的长.
考点:四边形综合题,平行线的判定
专题:几何综合题
分析:(1)分别证得DB∥ME和MN∥CB后利用两组对边分别相等的四边形是平行四边形即可证得结论;
(2)根据正方形BEFG,从而可得CM=1-x,然后得y=
(BG+MN)•BN即可.
(3)由已知易得四边形BGMP是平行四边形,要使四边形BGMP是菱形则BG=MG,可得x=
(1-x),解得x即可.
(2)根据正方形BEFG,从而可得CM=1-x,然后得y=
| 1 |
| 2 |
(3)由已知易得四边形BGMP是平行四边形,要使四边形BGMP是菱形则BG=MG,可得x=
| 2 |
解答:证明:(1)∵ABCD、BEFG是正方形
∴∠CBA=∠FEB=90°,∠ABD=∠BEG=45°,
∴DB∥ME(同位角相等,两直线平行).
∵MN⊥AB,CB⊥AB,
∴MN∥CB.
∴四边形MPBG是平行四边形;
(2)∵正方形BEFG,
∴BG=BE=x.
∵∠CMG=∠BEG=45°,
∴CG=CM=BN=1-x.
∴y=
(GB+MN)•BN=
(1+x)(1-x)=
-
x2(0<x<1);
(3)∵四边形BGMP是菱形,
∴BG=MG,
∴x=
(1-x),
∴x=2-
,
∴BE=2-
.
∴∠CBA=∠FEB=90°,∠ABD=∠BEG=45°,
∴DB∥ME(同位角相等,两直线平行).
∵MN⊥AB,CB⊥AB,
∴MN∥CB.
∴四边形MPBG是平行四边形;
(2)∵正方形BEFG,
∴BG=BE=x.
∵∠CMG=∠BEG=45°,
∴CG=CM=BN=1-x.
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵四边形BGMP是菱形,
∴BG=MG,
∴x=
| 2 |
∴x=2-
| 2 |
∴BE=2-
| 2 |
点评:此题考查了四边形的综合知识,较复杂,但充分利用题目所给的条件,根据四边形性质列出方程即可解答.解答此题,不要局限于一种方法,可以多试几种方法,以提高解题的“含金量”.

练习册系列答案
相关题目
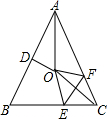 如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )| A、45° | B、50° |
| C、55° | D、60° |
 某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.
某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销. 解不等式组
解不等式组