题目内容
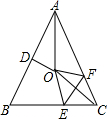 如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )| A、45° | B、50° |
| C、55° | D、60° |
考点:翻折变换(折叠问题),线段垂直平分线的性质,等腰三角形的性质
专题:
分析:作辅助线,由∠BAC的平分线与线段AB的中垂线交于点O,可求出∠OBM,∠OCM的值,再求出BOM和∠COM的值,由折叠性求出∠OEM,即可求出∠CEF.
解答: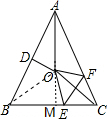
解:如图,延长AO交BC于点M,连接BO,
∵等腰△ABC中,AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=(180°-50°)÷2=65°,
∵AO是∠BAC的平分线,
∴∠BAO=25°,
又∵OD是AB的中垂线,
∴∠OBA=∠OAB=25°,
∴∠OBM=∠OCM=60°-25°=40°,
∴∠BOM=∠COM=90°-40°=50°,
由折叠性可知,∠OCM=∠COE,
∴∠MOE=∠COM-∠COE=50°-40°=10°,
∴∠OEM=90°-10°=80°,
∵由折叠性可知,∠OEF=∠CEF,
∴∠CEF=(180°-80°)÷2=50°.
故选:B.

解:如图,延长AO交BC于点M,连接BO,
∵等腰△ABC中,AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=(180°-50°)÷2=65°,
∵AO是∠BAC的平分线,
∴∠BAO=25°,
又∵OD是AB的中垂线,
∴∠OBA=∠OAB=25°,
∴∠OBM=∠OCM=60°-25°=40°,
∴∠BOM=∠COM=90°-40°=50°,
由折叠性可知,∠OCM=∠COE,
∴∠MOE=∠COM-∠COE=50°-40°=10°,
∴∠OEM=90°-10°=80°,
∵由折叠性可知,∠OEF=∠CEF,
∴∠CEF=(180°-80°)÷2=50°.
故选:B.
点评:本题主要考查了折叠问题,中垂线及等腰三角形的性质,解题的关键是能正确作出辅助线..

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
微电子技术的不断进步,使半导体材料的加工尺寸大幅度缩小.某种电子元件的面积大约为0.000 000 71平方毫米,将0.000 000 71写成科学记数法表示为( )
| A、0.71×10-8 |
| B、7.1×10-6 |
| C、7.1×10-7 |
| D、7.1×10-8 |
下列调查方式,你认为最合适的是( )
| A、日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式 |
| B、旅客上飞机前的安检,采用抽样调查方式 |
| C、了解北京市居民日平均用水量,采用全面调查方式 |
| D、了解北京市每天的流动人口数,采用抽样调查方式 |
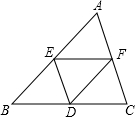 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )| A、5 | B、10 | C、15 | D、20 |
在平面直角坐标系中,点P(-1,4)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
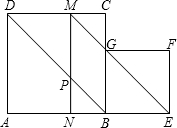 如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.
如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.