题目内容
(1)解方程:
+
=1;
(2)解不等式组:
.
| x |
| x-1 |
| 1 |
| x |
(2)解不等式组:
|
考点:解分式方程,解一元一次不等式组
专题:计算题
分析:(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答:解:(1)去分母得:x2+x-1=x(x-1),即x2+x-1=x2-x,
解得:x=
,
经检验x=
是分式方程的解;
(2)
,
由①得:x≥1;
由②得:x<3,
则不等式组的解集为1≤x<3.
解得:x=
| 1 |
| 2 |
经检验x=
| 1 |
| 2 |
(2)
|
由①得:x≥1;
由②得:x<3,
则不等式组的解集为1≤x<3.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
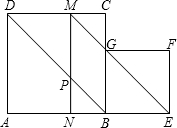 如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.
如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.