题目内容
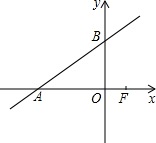 如图,已知直线y=
如图,已知直线y=| 5 |
| 12 |
(1)求点A、点B的坐标;
(2)设F是x轴上一动点,用尺规作图作出⊙P,使⊙P经过点B且与x轴相切于点F(不写作法和证明,保留作图痕迹);
(3)设(2)中所作的⊙P的圆心坐标为P(x,y),求y与x的函数关系式;
(4)是否存在这样的⊙P,既与x轴相切又与直线y=
| 5 |
| 12 |
考点:圆的综合题
专题:
分析:(1)令x=0以及y=0代入直线解析式可求出A,B的坐标;
(2)作出线段BF的垂直平分线进而过点F作垂直于x轴的直线交于点P,进而得出答案;
(3)做PD⊥y轴于D,根据勾股定理得出PB2=PD2+BD2,BP2=PD2+BD2.得出y与x的关系式即可;
(4)依题意可得AB2=OA2+OB2=AF2=132,求出关于x的值代入解析式,求出y值即可,求出点P的坐标.
(2)作出线段BF的垂直平分线进而过点F作垂直于x轴的直线交于点P,进而得出答案;
(3)做PD⊥y轴于D,根据勾股定理得出PB2=PD2+BD2,BP2=PD2+BD2.得出y与x的关系式即可;
(4)依题意可得AB2=OA2+OB2=AF2=132,求出关于x的值代入解析式,求出y值即可,求出点P的坐标.
解答: 解:(1)令y=0得x=-12,令x=0得,y=5,
解:(1)令y=0得x=-12,令x=0得,y=5,
∴A(-12,0),B(0,5);
(2)如图:
(3)如图:过点P作PD⊥y轴于D,则PD=|x|,BD=|5-y|,PB=PF=y,
∵△BDP为直角三角形,
∴BP2=PD2+BD2,
即|y|2=|x|2+|5-y|2,
y2=x2+(5-y)2,
∴y与x的函数关系为y=
x2+
;
(4)存在.
解:∵AO=12,BO=5,
∴AB=
=13,
∵⊙P与x轴相切于点F,且与直线l相切于点B,
∴AB=AF,
∵AB2=OA2+OB2=132,
∴AF2=132,
∵AF=|x+1|,
∴(x+12)2=132,
∴x1=-25,x2=1,
把x=-25,x=1代入y=
x2+
,
得y=65或y=2.6,
∴点P的坐标为(-25,65)或(1,2.6).
 解:(1)令y=0得x=-12,令x=0得,y=5,
解:(1)令y=0得x=-12,令x=0得,y=5,∴A(-12,0),B(0,5);
(2)如图:
(3)如图:过点P作PD⊥y轴于D,则PD=|x|,BD=|5-y|,PB=PF=y,
∵△BDP为直角三角形,
∴BP2=PD2+BD2,
即|y|2=|x|2+|5-y|2,
y2=x2+(5-y)2,
∴y与x的函数关系为y=
| 1 |
| 10 |
| 5 |
| 2 |
(4)存在.
解:∵AO=12,BO=5,
∴AB=
| AO2+BO2 |
∵⊙P与x轴相切于点F,且与直线l相切于点B,
∴AB=AF,
∵AB2=OA2+OB2=132,
∴AF2=132,
∵AF=|x+1|,
∴(x+12)2=132,
∴x1=-25,x2=1,
把x=-25,x=1代入y=
| 1 |
| 10 |
| 5 |
| 2 |
得y=65或y=2.6,
∴点P的坐标为(-25,65)或(1,2.6).
点评:本题考查的是圆的综合以及一次函数的图形与应用的有关知识以及考生作图能力,难度中等.

练习册系列答案
相关题目
 如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.
如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点. 如图,C是线段AB的中点,∠1=∠2=∠3,CD=CE.
如图,C是线段AB的中点,∠1=∠2=∠3,CD=CE.
