题目内容
 如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.
如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.(1)求证:△BCE≌△FDE;
(2)连结BD,CF,则△BDE和△FCE全等吗?为什么?
考点:全等三角形的判定与性质
专题:
分析:(1)根据平行线性质得出∠F=∠EBC,根据全等三角形的判定推出即可;
(2)根据全等得出BE=EF,根据全等三角形的判定推出即可.
(2)根据全等得出BE=EF,根据全等三角形的判定推出即可.
解答:(1)证明:∵AF∥BC,
∴∠F=∠EBC,
∵点E是CD的中点,
∴DE=CE,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(AAS);
(2)解:△BDE和△FCE全等,
理由是:∵△BCE≌△FDE;
∴BE=EF,
在△BDE和△FCE中
∴△BDE≌△FCE(SAS).
∴∠F=∠EBC,
∵点E是CD的中点,
∴DE=CE,
在△BCE和△FDE中,
|
∴△BCE≌△FDE(AAS);
(2)解:△BDE和△FCE全等,

理由是:∵△BCE≌△FDE;
∴BE=EF,
在△BDE和△FCE中
|
∴△BDE≌△FCE(SAS).
点评:本题考查了全等三角形的性质和判定,平行线的性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
 在长方形纸片ABCD中,AD=4cm,AB=8cm,按如图方式折叠.使点B与点D重合,则折痕EF=
在长方形纸片ABCD中,AD=4cm,AB=8cm,按如图方式折叠.使点B与点D重合,则折痕EF= 点A,B,C,D的位置如图,按下列要求画出图形.
点A,B,C,D的位置如图,按下列要求画出图形. 如图,⊙O是△ABC的外接圆,AF平分∠BAC交BC于点E,交⊙O于点F,BD平分∠ABC交AF于点D,过点F作FH∥BC.
如图,⊙O是△ABC的外接圆,AF平分∠BAC交BC于点E,交⊙O于点F,BD平分∠ABC交AF于点D,过点F作FH∥BC.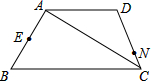 如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AB中点,请在对角线AC上找一点M使EM+MN的值最小,并求出EM+MN的最小值.
如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AB中点,请在对角线AC上找一点M使EM+MN的值最小,并求出EM+MN的最小值.


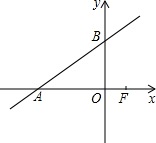 如图,已知直线y=
如图,已知直线y=