题目内容
如图在等腰Rt△A0B0C0中,A0(0,0)、C0(-12,0),B0C0⊥A0C0且B0C0=A0C0,以点P(9,0)为圆心,PO为半径的作⊙P,△A0B0C0以每秒钟一个单位的速度沿x轴向右移动,移动时间记为t秒,移动的三角形记为△ABC.(点A0对应A,点B0对应B,点C0对应C)
(1)如图,若点A为⊙P与x轴的另一个交点,BO交⊙P于D,AD交BC于E.
①求证:AE=BO;
②过C作CM⊥AE于M,交AB于N,求证:∠AEC=∠BEN;
(2)若F为AB边上的点,且AF=8
,若线段AF与⊙P有且只有一个公共点,求t的取值范围.

(1)如图,若点A为⊙P与x轴的另一个交点,BO交⊙P于D,AD交BC于E.
①求证:AE=BO;
②过C作CM⊥AE于M,交AB于N,求证:∠AEC=∠BEN;
(2)若F为AB边上的点,且AF=8
| 2 |

考点:圆的综合题,全等三角形的判定与性质,勾股定理,切线的性质,相似三角形的判定与性质,特殊角的三角函数值
专题:综合题
分析:(1)如图1,要证AE=BO,只需证到△OCB≌△ECA即可.
(2)如图2,易证△ACN∽△AOB,从而可求出AN及BN的长,进而可证到△EBN∽△CAN,则有∠BEN=∠ACN.易证∠AEC=∠ACN,即可得到∠AEC=∠BEN.
(3)只需先考虑临界位置[点F在⊙P上(图3、图4)、点A在⊙P上(图2)、线段AF与⊙P相切(图5)]所对应的t的值,就可求出符合条件的t的取值范围.
(2)如图2,易证△ACN∽△AOB,从而可求出AN及BN的长,进而可证到△EBN∽△CAN,则有∠BEN=∠ACN.易证∠AEC=∠ACN,即可得到∠AEC=∠BEN.
(3)只需先考虑临界位置[点F在⊙P上(图3、图4)、点A在⊙P上(图2)、线段AF与⊙P相切(图5)]所对应的t的值,就可求出符合条件的t的取值范围.
解答: 解:(1)证明:如图1,
解:(1)证明:如图1,
∵OA是⊙P的直径,
∴∠ODA=90°,即∠DOA+∠DAO=90°.
∵∠BCA=90°,即∠BOC+∠OBC=90°.
∴∠DAO=∠OBC.
在△OCB和△ECA中,
.
∴△OCB≌△ECA.
∴BO=AE.
(2)证明:如图2,
∵A0(0,0)、C0(-12,0),∴A0C0=12.
∴BC=AC=A0C0=12.
∴AB=
=12
.
∵点P的坐标为(9,0),
∴OA=2OP=18.
∴OC=6.
∵△OCB≌△ECA,
∴OC=EC=6.
∴BE=6.
∵CM⊥AE,即∠AMC=90°,∠ODA=90°,
∴∠AMC=∠ODA.
∴CN∥OB.
∴△ACN∽△AOB.
∴
=
.
∴AN=8
.
∴BN=4
.
∵
=
=
,
=
=
,
∴
=
.
∵∠EBN=∠CAN=45°,
∴△EBN∽△CAN.
∴∠BEN=∠ACN.
∵∠AEC=90°-∠EAC=∠ACN,
∴∠AEC=∠BEN.
(3)①当点F在⊙P上时,
Ⅰ.如图3,过点F作FH⊥OA于H,连接PF.
在Rt△AHF中,
∵AH=8,∠FAH=45°,AF=8
,
∴FH=AF•sin∠FAH=8
×
=8,
AH=AF•cos∠FAH=8
×
=8.
在Rt△PHF中,
PH=
=
=
.
∴PA=AH-PH=8-
.
∴A0A=OA=OP+PA=9+8-
=17-
.
此时,t=17-
.
Ⅱ.如图4,过点F作FH⊥OA于H,连接PF.
同理可得:AH=8,PH=
.
∴PA=AH+PH=8+
.
∴A0A=OA=OP+PA=9+8+
=17+
.
此时,t=17+
.
②当点A在⊙P上时,如图2.
则有A0A=OA=18.
此时,t=18.
③当线段AF与⊙P相切于点Q时,连接PQ,如图5.
则有PQ=9,∠PQA=90°.
在Rt△PQA中,
sin∠QAP=
=
=
.
解得:PA=9
.
∴A0A=OA=OP+PA=9+9
.
此时,t=9+9
.
综上所述:当线段AF与⊙P有且只有一个公共点时,t的取值范围是0≤t≤17-
或18≤t<17+
或t=9+9
.
 解:(1)证明:如图1,
解:(1)证明:如图1,∵OA是⊙P的直径,
∴∠ODA=90°,即∠DOA+∠DAO=90°.
∵∠BCA=90°,即∠BOC+∠OBC=90°.
∴∠DAO=∠OBC.
在△OCB和△ECA中,
|
∴△OCB≌△ECA.
∴BO=AE.
(2)证明:如图2,
∵A0(0,0)、C0(-12,0),∴A0C0=12.
∴BC=AC=A0C0=12.
∴AB=
| BC2+CA2 |
| 2 |
∵点P的坐标为(9,0),
∴OA=2OP=18.

∴OC=6.
∵△OCB≌△ECA,
∴OC=EC=6.
∴BE=6.
∵CM⊥AE,即∠AMC=90°,∠ODA=90°,
∴∠AMC=∠ODA.
∴CN∥OB.
∴△ACN∽△AOB.
∴
| AN |
| AB |
| AC |
| AO |
∴AN=8
| 2 |
∴BN=4
| 2 |
∵
| BN |
| BE |
4
| ||
| 6 |
2
| ||
| 3 |
| AN |
| AC |
8
| ||
| 12 |
2
| ||
| 3 |
∴
| BN |
| BE |
| AN |
| AC |
∵∠EBN=∠CAN=45°,
∴△EBN∽△CAN.
∴∠BEN=∠ACN.

∵∠AEC=90°-∠EAC=∠ACN,
∴∠AEC=∠BEN.
(3)①当点F在⊙P上时,
Ⅰ.如图3,过点F作FH⊥OA于H,连接PF.
在Rt△AHF中,
∵AH=8,∠FAH=45°,AF=8
| 2 |
∴FH=AF•sin∠FAH=8
| 2 |
| ||
| 2 |

AH=AF•cos∠FAH=8
| 2 |
| ||
| 2 |
在Rt△PHF中,
PH=
| PF2-FH2 |
| 92-82 |
| 17 |
∴PA=AH-PH=8-
| 17 |
∴A0A=OA=OP+PA=9+8-
| 17 |
| 17 |
此时,t=17-
| 17 |
Ⅱ.如图4,过点F作FH⊥OA于H,连接PF.
同理可得:AH=8,PH=
| 17 |
∴PA=AH+PH=8+
| 17 |
∴A0A=OA=OP+PA=9+8+
| 17 |
| 17 |

此时,t=17+
| 17 |
②当点A在⊙P上时,如图2.
则有A0A=OA=18.
此时,t=18.
③当线段AF与⊙P相切于点Q时,连接PQ,如图5.
则有PQ=9,∠PQA=90°.
在Rt△PQA中,
sin∠QAP=
| PQ |
| PA |
| 9 |
| PA |
| ||
| 2 |
解得:PA=9
| 2 |
∴A0A=OA=OP+PA=9+9
| 2 |
此时,t=9+9
| 2 |
综上所述:当线段AF与⊙P有且只有一个公共点时,t的取值范围是0≤t≤17-
| 17 |
| 17 |
| 2 |
点评:本题考查了切线的性质、全等三角形的判定与性质、相似三角形的判定与性质、特殊角的三角函数值、勾股定理等知识,还考查了分类讨论的数学思想,而考虑临界位置是求未知数取值范围常用的一种方法,应掌握它.

练习册系列答案
相关题目

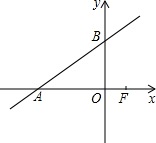 如图,已知直线y=
如图,已知直线y=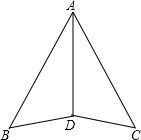 已知:如图,AD平分∠BAC,∠B=∠C.求证:BD=CD.
已知:如图,AD平分∠BAC,∠B=∠C.求证:BD=CD.