题目内容
 如图,两相交圆的公共弦AB的长为2
如图,两相交圆的公共弦AB的长为2| 3 |
考点:相交两圆的性质
专题:
分析:根据内接多边形的性质分别求得两圆的半径,然后根据圆的面积公式求这两圆的面积之比.
解答: 解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.
解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.
∵AB为⊙O′内接正六边形的一边,
∴△O′AB为等边三角形,
∴O′A=AB=2
.
又∵AB分别为⊙O的内接正三角形,
∴AD=
,∠AOB=2∠ACB=120°,
∴∠AOD=60°,
∴OA=
=
=2,
∴这两圆的面积之比为:πO′A2:πOA2=O′A2:OA2=2
:2=
:1.
 解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.
解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.∵AB为⊙O′内接正六边形的一边,
∴△O′AB为等边三角形,
∴O′A=AB=2
| 3 |
又∵AB分别为⊙O的内接正三角形,
∴AD=
| 3 |
∴∠AOD=60°,
∴OA=
| AD |
| sin60° |
| ||||
|
∴这两圆的面积之比为:πO′A2:πOA2=O′A2:OA2=2
| 3 |
| 3 |
点评:考查了相交两圆的性质、等边三角形的性质以及解直角三角形.此题实际上求两圆的半径之比.

练习册系列答案
相关题目
一个角和它的余角的比是1:2,则这个角的补角的度数是( )
| A、150° | B、120° |
| C、110° | D、70° |
 如图,AB为⊙O的直径,PF切⊙O于A,△ABC是⊙O的内接三角形,AC=8,过C作CF与AB、PA、⊙O分别交于E、D、F,CE:ED=6:5,AE:EB=2:3,求:
如图,AB为⊙O的直径,PF切⊙O于A,△ABC是⊙O的内接三角形,AC=8,过C作CF与AB、PA、⊙O分别交于E、D、F,CE:ED=6:5,AE:EB=2:3,求: 如图,AB•AE=AC•AD,∠1=∠2,求证:∠B=∠D.
如图,AB•AE=AC•AD,∠1=∠2,求证:∠B=∠D.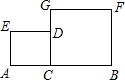 如图,已知线段AB=6,在线段AB上有一点C(不同于A、B),分别以AC、BC为边在AB同侧作正方形ACDE、CBFG,设AC=x.
如图,已知线段AB=6,在线段AB上有一点C(不同于A、B),分别以AC、BC为边在AB同侧作正方形ACDE、CBFG,设AC=x.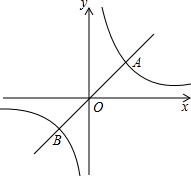 如图,定义:若双曲线y=
如图,定义:若双曲线y= 如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.
如图,线段AB=6,点O是线段AB上一点,C,D分别是线段OA,OB的中点,小华据此轻松地求得CD=3.他在反思过程中突发奇想:若点O运动到AB的延长线上,原有的结论“CD=3”是否仍然成立?请帮小华画出图形并说明理由.