题目内容
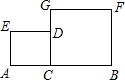如图，已知线段AB=6，在线段AB上有一点C（不同于A、B），分别以AC、BC为边在AB同侧作正方形ACDE、CBFG，设AC=x．（1）求两个正方形的面积之和S；
（2）试探求点C在线段AB的什么位置时，S最小，并求出S的最小值．
考点：正方形的性质,二次函数的最值
专题：
分析：（1）表示出BC，再根据正方形的面积公式列式整理即可；
（2）把S与x的关系式整理成顶点式形式，然后根据二次函数的最值问题解答．
（2）把S与x的关系式整理成顶点式形式，然后根据二次函数的最值问题解答．
解答：解：（1）∵AB=6，AC=x，
∴BC=6-x，
∴S=x2+（6-x）2=2x2-12x+36；
（2）∵S=2x2-12x+36，
=2（x2-6x+9）+18，
=2（x-3）2+18，
∴当x=3时，S有最小值18．
∴BC=6-x，
∴S=x2+（6-x）2=2x2-12x+36；
（2）∵S=2x2-12x+36，
=2（x2-6x+9）+18，
=2（x-3）2+18，
∴当x=3时，S有最小值18．
点评：本题考查了正方形的性质，二次函数的最值问题，（2）把函数解析式整理成顶点式求解更简便．
练习册系列答案
相关题目
如图，AB，BC，CD都与半圆相切，A、D是切点．其中AB=4，CD=9，BC=13，则半圆的半径是（ ）| A、12 | B、10 | C、8 | D、6 |
已知：如图，AB、CD是⊙O的两条平行切线，A、C是切点，⊙O的另一条切线BD与
如图，两相交圆的公共弦AB的长为2