Question

边长为6的正三角形的外接圆的周长是

 

．

Answer 1

考点：正多边形和圆

专题：

分析：根据题意画出图形，先求出边长为6的正三角形的外接圆的半径，再求出其周长即可．

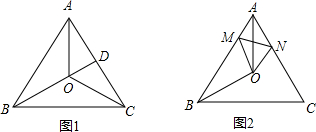
解答：解：如图所示，
连接OB、OC，过O作OD⊥BC于D，
∵△ABC是边长为6的等边三角形，BC=6，
∴∠BOC=

360°

3

=120°，∠BOD=

1

2

∠BOC=60°，BD=3，
∴OB=

BD

sin60°

=

3

3 2

=2

3

，
∴外接圆的周长=2π×2

3

=4

3

π．
故答案为：4

3

π．

点评：本题考查的是正多边形和圆，根据题意画出图形，利用数形结合求解是解答此题的关键．