题目内容
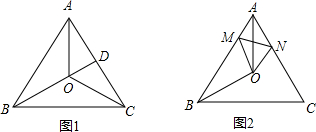
如图1,等边△ABC中,BD是高,CO平分∠ACB,交BD于点O.
(1)求证:BO=2DO;
(2)连接AO,求∠AOB的度数;
(3)将图1中的∠DOC绕点O逆时针方向旋转a角度(60°<a<120°)时,如图2,∠DOC的两边分别交AB于点M,交AC于点N,连接MN,求证:∠BMO=∠NMO.
(1)求证:BO=2DO;
(2)连接AO,求∠AOB的度数;
(3)将图1中的∠DOC绕点O逆时针方向旋转a角度(60°<a<120°)时,如图2,∠DOC的两边分别交AB于点M,交AC于点N,连接MN,求证:∠BMO=∠NMO.

考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:(1)证明点O为△ABC的重心,即可解决问题.
(2)证明∠BAO+∠ABO=60°,借助三角形的内角和定理即可解决问题.
(3)如图,作辅助线;证明△MOE∽△NOF,得到
=
,根据OE=OF,得到
=
;借助∠NOF=∠MON=60°,得到△NOF∽△MON,即可解决问题.
(2)证明∠BAO+∠ABO=60°,借助三角形的内角和定理即可解决问题.
(3)如图,作辅助线;证明△MOE∽△NOF,得到
| ON |
| OM |
| NF |
| EO |
| ON |
| OM |
| NF |
| OF |
解答: 解:(1)∵△ABC是等边三角形,BD是高,CO平分∠ACB,
解:(1)∵△ABC是等边三角形,BD是高,CO平分∠ACB,
∴点O为△ABC的重心,
∴BO=2DO.
(2)∵△ABC是等边三角形,且点O为其重心,
∴∠BAC=∠ABC=60°,AO、BO分别平分∠BAC、∠ABC,
∴∠BAO+∠ABO=30°+30°=60°,∠AOB=180°-60°=120°,
即∠AOB的度数为120°.
(3)过点O作EF∥BC;则△AEF为等边三角形,AO平分∠EAF;
∴∠AEF=∠AFE=60°,EO=FO;
∵∠MOF=∠AEO+∠EMO=∠MON+∠NOF,且∠MON=60°,
∴∠NOF=∠PME,
∴△MOE∽△NOF,
∴
=
,而OE=OF,
∴
=
,且∠NOF=∠MON=60°,
∴△NOF∽△MON,
∴∠NOF=∠OMN,
∴∠BMO=∠NMO.
 解:(1)∵△ABC是等边三角形,BD是高,CO平分∠ACB,
解:(1)∵△ABC是等边三角形,BD是高,CO平分∠ACB,∴点O为△ABC的重心,
∴BO=2DO.
(2)∵△ABC是等边三角形,且点O为其重心,
∴∠BAC=∠ABC=60°,AO、BO分别平分∠BAC、∠ABC,
∴∠BAO+∠ABO=30°+30°=60°,∠AOB=180°-60°=120°,
即∠AOB的度数为120°.
(3)过点O作EF∥BC;则△AEF为等边三角形,AO平分∠EAF;
∴∠AEF=∠AFE=60°,EO=FO;
∵∠MOF=∠AEO+∠EMO=∠MON+∠NOF,且∠MON=60°,
∴∠NOF=∠PME,
∴△MOE∽△NOF,
∴
| ON |
| OM |
| NF |
| EO |
∴
| ON |
| OM |
| NF |
| OF |
∴△NOF∽△MON,
∴∠NOF=∠OMN,
∴∠BMO=∠NMO.
点评:该题主要考查了等边三角形的性质、相似三角形的判定及其性质等几何知识点的应用问题;解题的关键是作辅助线,灵活运用相似三角形的判定及其性质等几何知识点来分析、推理、证明.

练习册系列答案
相关题目
下列计算正确的是( )
| A、3x3+2x2=5x5 |
| B、5ab+4c=9abc |
| C、8x3y-9xy3=x3y |
| D、25a-24a=24a |
下列说法正确的是( )
| A、近似数25.0与25的精确度相同 |
| B、近似数0.003020有四个有效数字 |
| C、近似数2.50与25的有效数数字相同 |
| D、0.3998精确到百分位是0.4 |
 如图,点C在线段AB上一点,AC=8cm,CB=6cm,点M,N分别是AC,BC的中点.
如图,点C在线段AB上一点,AC=8cm,CB=6cm,点M,N分别是AC,BC的中点. 如图,在△ABC中,AB=AC,D是BC中点,BF⊥AC,垂足为F,BF交AD于E,且∠BAC=45°,求证:EF=CF.
如图,在△ABC中,AB=AC,D是BC中点,BF⊥AC,垂足为F,BF交AD于E,且∠BAC=45°,求证:EF=CF.