题目内容
20.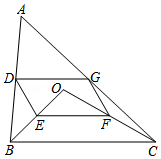 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;
(2)如果∠BOC=90°,∠OCB=30°,OB=2,求EF的长.
分析 (1)根据三角形中位线的性质可得DG∥BC,DG=$\frac{1}{2}$BC,EF∥BC,EF=$\frac{1}{2}$BC,进而可得DG∥EF,DG=EF,再由一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据直角三角形的性质可得CB=2OB=4,再根据三角形中位线的性质可得EF=$\frac{1}{2}$BC=2.
解答 (1)证明:∵AB、OB、OC、AC的中点分别为D、E、F、G,
∴DG∥BC,DG=$\frac{1}{2}$BC,EF∥BC,EF=$\frac{1}{2}$BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:∵∠BOC=90°,∠OCB=30°,OB=2,
∴在Rt△BOC中,CB=2OB=4,
∴EF=$\frac{1}{2}$BC=2.
点评 此题主要考查了中点四边形和三角形中位线的性质,关键是掌握一组对边平行且相等的四边形是平行四边形,三角形的中位线平行于第三边且等于第三边的一半

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
10.下列运算正确的是( )
| A. | (-2ab)•(-3ab)2=-54a4b4 | B. | 5x2•(3x3)2=15x12 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (2×10a)($\frac{1}{2}$×10a)=102a |
8.如果(a-1)x2+ax+a2-1=0是关于x的一元二次方程,那么必有( )
| A. | a≠0 | B. | a≠1 | C. | a≠-1 | D. | a=±-1 |
5.下列语句正确的是( )
| A. | 一条直线可以看成一个平角 | |
| B. | 周角是一条射线 | |
| C. | 角是由一条射线旋转而成的 | |
| D. | 角是由公共端点的两条射线组成的图形 |
12. 如图所示,已知CD平分∠ACB,DE∥AC,∠1=30°,则∠2=( )
如图所示,已知CD平分∠ACB,DE∥AC,∠1=30°,则∠2=( )
 如图所示,已知CD平分∠ACB,DE∥AC,∠1=30°,则∠2=( )
如图所示,已知CD平分∠ACB,DE∥AC,∠1=30°,则∠2=( )| A. | 35° | B. | 30° | C. | 50° | D. | 60° |
9.若a2-2a-2=0,则(a-1)2=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
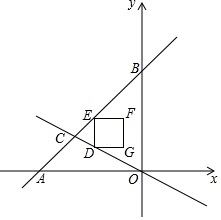 如图,直线y=x+6与x轴交于点A,与y轴交于点B,与直线y=-$\frac{1}{2}$x交于点C,D为线段OC上的动点,D与C,O不重合,作DE∥OB交AB于E,以DE为边在DE的右侧作正方形DEFO,正方形DEFG与△BOC重叠部分的面积为S,D点的横坐标为x,求S与x的函数关系式.
如图,直线y=x+6与x轴交于点A,与y轴交于点B,与直线y=-$\frac{1}{2}$x交于点C,D为线段OC上的动点,D与C,O不重合,作DE∥OB交AB于E,以DE为边在DE的右侧作正方形DEFO,正方形DEFG与△BOC重叠部分的面积为S,D点的横坐标为x,求S与x的函数关系式.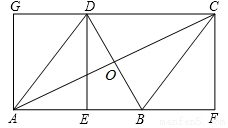 如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O,连接AD,BC.
如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O,连接AD,BC.