题目内容
10.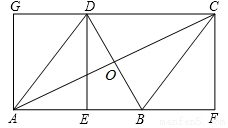 如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O,连接AD,BC.
如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O,连接AD,BC.(1)求证:四边形ABCD是菱形;
(2)若E为AB的中点,DE⊥AB,求∠BDC的度数.
分析 (1)只要证明AB=BC=CD=DA即可;
(2)只要证明△ADB是等边三角形即可解决问题;
解答 (1)证明:∵BD垂直平分AC,
∴OA=OC,AD=CD,AB=BC,
∵四边形AFCG是矩形,
∴CG∥AF,
∴∠CDO=∠ABO,∠DCO=∠BAO,
∴△COD≌△AOB,
∴CD=AB,
∴AB=BC=CD=DA,
∴四边形ABCD是菱形.
(2)∵E为AB中点,DE⊥AB,
∴DE垂直平分AB,
∴AD=DB,
∵AD=AB,
∴△ADB为等边三角形,
∴∠DBA=60°,
∵CD∥AB,
∴∠BDC=∠DBA=60°.
点评 本题考查矩形的性质、菱形的判定、等边三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.要使分式$\frac{1}{2+a}$有意义,则a应满足的条件是( )
| A. | a≠-2 | B. | a>0 | C. | a≠0 | D. | a≠2 |
18.已知平行四边形ABCD中,∠B=5∠A,则∠C=( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
15. 若∠1与∠2互补,∠3=130°,则∠4等于( )
若∠1与∠2互补,∠3=130°,则∠4等于( )
 若∠1与∠2互补,∠3=130°,则∠4等于( )
若∠1与∠2互补,∠3=130°,则∠4等于( )| A. | 75° | B. | 50° | C. | 45≤ | D. | 135° |
19.以下列所给线段长为三边,能构成三角形的是( )
| A. | 1cm、2cm、3cm | B. | 3cm、4cm、6cm | C. | 1cm、1cm、3cm | D. | 2cm、3cm、7cm |
20.计算:(x2)3=( )
| A. | x9 | B. | x6 | C. | x5 | D. | x |
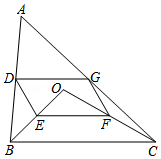 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.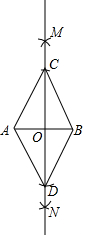 小明在白纸上作一个菱形,他按如下步骤:
小明在白纸上作一个菱形,他按如下步骤: