题目内容
15.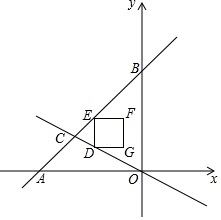 如图,直线y=x+6与x轴交于点A,与y轴交于点B,与直线y=-$\frac{1}{2}$x交于点C,D为线段OC上的动点,D与C,O不重合,作DE∥OB交AB于E,以DE为边在DE的右侧作正方形DEFO,正方形DEFG与△BOC重叠部分的面积为S,D点的横坐标为x,求S与x的函数关系式.
如图,直线y=x+6与x轴交于点A,与y轴交于点B,与直线y=-$\frac{1}{2}$x交于点C,D为线段OC上的动点,D与C,O不重合,作DE∥OB交AB于E,以DE为边在DE的右侧作正方形DEFO,正方形DEFG与△BOC重叠部分的面积为S,D点的横坐标为x,求S与x的函数关系式.
分析 解:设D(x,-$\frac{1}{2}$x),根据DE∥OB,得到E(x,x+6),求得DE=$\frac{3}{2}$x+6,当GF落在y轴上时,解方程组得到C(-4,2),求得x=-$\frac{12}{5}$,当-4<x≤-$\frac{12}{5}$时,如图1,当-$\frac{12}{5}$<x<0时,如图3,根据矩形的面积公式即可得到结论.
解答 解:设D(x,-$\frac{1}{2}$x),
∵DE∥OB,
∴E(x,x+6),
∴DE=$\frac{3}{2}$x+6,
当GF落在y轴上时,
∵DE=DG,如图2,
解$\left\{\begin{array}{l}{y=x+6}\\{y=-\frac{1}{2}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=-4}\\{y=2}\\{\;}\end{array}\right.$,
∴C(-4,2),
∴$\frac{3}{2}$x+6=-x,
∴x=-$\frac{12}{5}$,
当-4<x≤-$\frac{12}{5}$时,如图1,
S=S四边形DEFG=DE2=$\frac{9}{4}$x2+18x+36;
当-$\frac{12}{5}$<x<0时,如图3,
重叠部分为矩形DENM,
∴S=S四边形DENM=DE•DM=-$\frac{3}{2}$x2-6x;
综上所述:S=$\left\{\begin{array}{l}{\frac{9}{4}{x}^{2}+18x+36(-4<x≤-\frac{12}{5})}\\{-\frac{3}{2}{x}^{2}-6x(-\frac{12}{5}<x<0)}\end{array}\right.$.
点评 本题考查了两直线平行与相交,正方形的性质,矩形的判定和性质,正确的识别图象是解题的关键.

| A. | $\sqrt{({-9)}^{2}}$=-9 | B. | $\sqrt{25}$=±5 | C. | $\root{3}{-27}$=-3 | D. | (-$\sqrt{2}$)2=-2 |
 某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为( )人.
某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为( )人.| A. | 120 | B. | 110 | C. | 100 | D. | 80 |
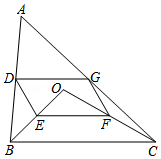 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.