题目内容
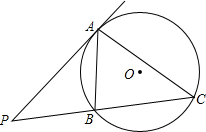 如图,P是⊙O外一点,过P作PA切⊙O于A,PC为⊙O的割线,交⊙O于点B,求证:AB2:AC2=PB:PC.
如图,P是⊙O外一点,过P作PA切⊙O于A,PC为⊙O的割线,交⊙O于点B,求证:AB2:AC2=PB:PC.考点:切线的性质,相似三角形的判定与性质
专题:证明题
分析:由PA切⊙O于A,PC为⊙O的割线,根据弦切角定理,可得∠PAB=∠C,继而可证得△PAB∽△PCA,然后由相似三角形面积比等于相似比的平方,得到S△PAB:S△PCA=AB2:AC2,又由等高三角形的面积的比等于对应底的比,可得S△PAB:S△PCA=PB:PC,继而证得结论.
解答:证明:∵PA切⊙O于A,PC为⊙O的割线,
∴∠PAB=∠C,
∵∠P是公共角,
∴△PAB∽△PCA,
∴S△PAB:S△PCA=AB2:AC2,
∵S△PAB:S△PCA=PB:PC,
∴AB2:AC2=PB:PC.
∴∠PAB=∠C,
∵∠P是公共角,
∴△PAB∽△PCA,
∴S△PAB:S△PCA=AB2:AC2,
∵S△PAB:S△PCA=PB:PC,
∴AB2:AC2=PB:PC.
点评:此题考查了切线的性质、弦切角定理、相似三角形的判定与性质以及三角形面积比问题.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
下列条件中,不能判定四边形ABCD是平行四边形的是( )
| A、AB=CD,AD=BC |
| B、AB∥CD,AB=CD |
| C、AB=CD,AD∥BC |
| D、AB∥CD,AD∥BC |
 如图,在?ABCD中,AE⊥BC,垂足为E,如果∠D=48°,那么∠B与∠BAE的度数各是多少?
如图,在?ABCD中,AE⊥BC,垂足为E,如果∠D=48°,那么∠B与∠BAE的度数各是多少?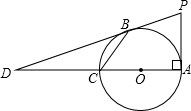 如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且
如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且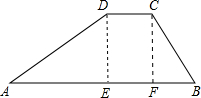 如图,一个水库大坝的横截面是梯形,其横截面的迎水坡AD的坡比为2:3,背水坡BC的坡比为4:3,大坝高DE为20m.坝顶宽CD为45m.求大坝的横截面积.
如图,一个水库大坝的横截面是梯形,其横截面的迎水坡AD的坡比为2:3,背水坡BC的坡比为4:3,大坝高DE为20m.坝顶宽CD为45m.求大坝的横截面积.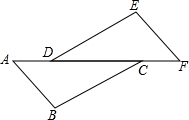 如图,△ABC与△DEF的点A、D、C、F在同一直线上,且AD=CF,BC=ED,∠BCA=∠EDF.
如图,△ABC与△DEF的点A、D、C、F在同一直线上,且AD=CF,BC=ED,∠BCA=∠EDF. 如图,两个同心圆都以O点为圆心,大圆的弦AB交小圆于C、D两点,若AB=3cm,CD=2cm,求圆环的面积.
如图,两个同心圆都以O点为圆心,大圆的弦AB交小圆于C、D两点,若AB=3cm,CD=2cm,求圆环的面积. 如图,D是四边形AEBC内一点,连接AD、BD,已知CA=CB,DA=DB,EA=EB.
如图,D是四边形AEBC内一点,连接AD、BD,已知CA=CB,DA=DB,EA=EB.