题目内容
7．
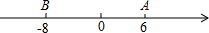已知数轴上两点A、B对应的数分别是6，-8，M、N为数轴上三个动点，点M从A点出发速度为每秒2个单位，点N从点B出发速度变为M点的3倍．（1）若点M向右运动，同时点N向左运动，求多长时间点M与点N相距54个单位？
（2）若点M、N同时都向右运动，求多长时间点M与点N相距4个单位？
分析 （1）设经过x秒点M与点N相距54个单位，由点M从A点出发速度为每秒2个单位，点N从点B出发速度为M点的3倍，得出2x+6x+14=54求出即可；
（2）首先设经过t秒点M与点N相距4个单位，得出（2t+6）-（6t-8）=4或（6t-82）-（2t+6）=4，进而求出即可．
解答 解：（1）设经过x秒点M与点N相距54个单位．
依题意可列方程为：2x+6x+14=54，
解方程，得x=5．
答：经过5秒点M与点N相距54个单位．（算术方法对应给分）
（2）设经过t秒点M与点N相距4个单位．
（2t+6）-（6t-8）=4或（6t-8）-（2t+6）=4，
解得t=2.5或t=4.5．
答：经过2.5或4.5秒时间点M与点N相距4个单位．
点评 此题主要考查了数轴、一元一次方程的应用，根据已知点运动速度得出以及距离之间的关系得出等式是解题关键．
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
某中学八（1）班共50名同学开展了“我为灾区献爱心”捐款活动．小明将捐款情况进行了统计，并绘制成如图的条形统计图．