Question

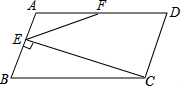如图，在平行四边形ABCD中，AB=5，BC=10，F为AD中点，CE⊥AB于点E，设∠ABC=α（60°≤α＜90°）．
（1）当α=90°时，求CE的长；
（2）当60°＜α＜90°时
①是否存在正整数k，使得∠EFD=k∠AEF？若存在，求出k值；若不存在，请说明理由．
②连接CF，当BE为何值时，CE²-CF²取最大值？

Answer 1

考点：四边形综合题

专题：

分析：（1）判定平行四边形ABCD是矩形后即可得到CE=CB=10；
（2）①连接CF并延长交BA的延长线于点G，首先证得△AFG≌△CFD，得到CF=GF，AG=CD，再根据CE⊥AB，F是GC边中点，得到EF=GF，从而得到∠EFD=∠EFC+∠CFD=2∠AEF
②设BE=x，根据AG=CD=AB=5，得到EG=AE+AG=5-x+5=10-x，然后分别在Rt△BCE中得到CE²=BC²-BE²=100-x²和在Rt△CEG中得到CG²=EG²+CE²=（10-x）²+100-x²=200-20x．然后代入CE²-CF²=100-x²-50+5x=-x2+5x+50=-（x-2.5 ）²+50+（2.5）²．

解答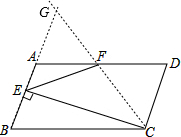：（1）∵四边形ABCD是平行四边形，
∴当∠ABC=α=90°时，四边形ABCD为矩形，
∵CE⊥AB，
∴点E与点B重合，
∴CE=CB=10；

（2）①存在k=3，使得∠EFD=k∠AEF．理由如下：
连接CF并延长交BA的延长线于点G，
∵F为AD的中点，
∴AF=FD．
在平行四边形ABCD中，AB∥CD，∴∠G=∠DCF．
在△AFG和△CFD中，
∵∠G=∠DCF，∠G=∠DCF，AF=FD，
∴△AFG≌△CFD（AAS）．
∴CF=GF，AG=CD．
∵CE⊥AB，F是GC边中点，
∴EF=GF．∴∠AEF=∠G．
∵AB=5，BC=10，点F是AD的中点，
∴AG=5，AF=AD=BC=5．
∴AG=AF，
∴∠AFG=∠G，
在△AFG中，∠EFC=∠AEF+∠G=2∠AEF，
又∵∠CFD=∠AFG，
∴∠CFD=∠AEF．
∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF，
因此，存在正整数k=3，使得∠EFD=3∠AEF．

（2）设BE=x，∵AG=CD=AB=5，
∴EG=AE+AG=5-x+5=10-x，
在Rt△BCE中，CE²=BC²-BE²=100-x²．
在Rt△CEG中，CG²=EG²+CE²=（10-x）²+100-x²=200-20x．
∵CF=GF（①中已证），
∴CF²=

CG2

4

=50-5x．
∴CE²-CF²=100-x²-50+5x=-x2+5x+50=-（x-2.5 ）²+50+（2.5）²．
∴当x=2.5，即点E是AB的中点时，CE²-CF²取最大值．

点评：本题考查了四边形的综合知识，解题的关键是了解特殊的四边形的性质，题目中用到了方程的数学思想，是中考的热点考点之一，应加强训练，难度较大．