题目内容
点P是抛物线y=x2上第一象限内的一点,A点坐标为(3,0),设P(x,y),在抛物线上求一点P′,使P′O=P′A.
考点:二次函数图象上点的坐标特征,线段垂直平分线的性质
专题:计算题
分析:作PB⊥OA于B,根据线段垂直平分线的性质得到OB=
OA=
,则点P的横坐标为
,然后根据二次函数图象上点的坐标特征求出对应的纵坐标,从而得到点P的坐标.
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:如图,
作PB⊥OA于B,
∵PO=PA,
∴OB=AB=
OA=
,
∴点P的横坐标为
,
把x=
代入y=x2得y=(
)2=
,
∴P点坐标为(
,
).

作PB⊥OA于B,
∵PO=PA,
∴OB=AB=
| 1 |
| 2 |
| 3 |
| 2 |
∴点P的横坐标为
| 3 |
| 2 |
把x=
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
∴P点坐标为(
| 3 |
| 2 |
| 9 |
| 4 |
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了线段垂直平分线的性质.

练习册系列答案
相关题目
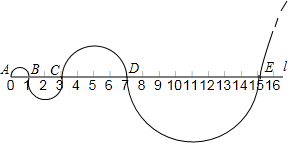 如图,从原点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆;…,按此规律,继续画半圆,则第5个半圆的面积为
如图,从原点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆;…,按此规律,继续画半圆,则第5个半圆的面积为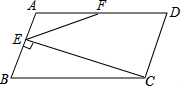 如图,在平行四边形ABCD中,AB=5,BC=10,F为AD中点,CE⊥AB于点E,设∠ABC=α(60°≤α<90°).
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD中点,CE⊥AB于点E,设∠ABC=α(60°≤α<90°).