题目内容
18.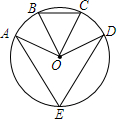 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )| A. | 46° | B. | 68° | C. | 69° | D. | 70° |
分析 先根据圆心角、弧、弦的关系求出∠AOD的度数,再由圆周角定理得出∠AED的度数即可.
解答 解:∵点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,
∴∠AOD=3∠BOC=3×46°=138°,
∴∠AED=$\frac{1}{2}$∠AOD=$\frac{1}{2}$×138°=69°,
故选C.
点评 本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.当n=1,2,3,4,5,…,2012,2013时,二次函数y=(n2+n)x2-(2n+1)x+1的图象与x轴所截的线段长度之和为( )
| A. | $\frac{2011}{2012}$ | B. | $\frac{2012}{2013}$ | C. | $\frac{2013}{2014}$ | D. | $\frac{2014}{2015}$ |
13.南昌市某路公交车共有10站,我们把上客人数记为“+”,把下客人数记为“-”,一次该路一辆公交车各站上、下人数列表如下:
(1)求表格中x的值;
(2)求在⑤、⑥站之间该公交车上的人数;
(3)问在哪两站之间,该公交车上的人数最多?并求最多人数.
| ①始发站 | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩终点站 | |
| 上客人数 | 9 | 8 | 10 | 12 | 14 | 13 | 11 | 6 | 7 | 0 |
| 下客人数 | 0 | -3 | -5 | -7 | -4 | -8 | -6 | -9 | x | -28 |
(2)求在⑤、⑥站之间该公交车上的人数;
(3)问在哪两站之间,该公交车上的人数最多?并求最多人数.
3.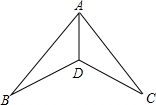 如图,下列条件中,不能证明△ABD≌△ACD的是( )
如图,下列条件中,不能证明△ABD≌△ACD的是( )
 如图,下列条件中,不能证明△ABD≌△ACD的是( )
如图,下列条件中,不能证明△ABD≌△ACD的是( )| A. | ∠B=∠C,BD=DC | B. | BD=DC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=DC |
8.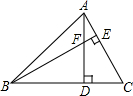 如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
 如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
 如图,△ABC中,BD平分∠ABC,∠ABC=60°,∠C=40°,求∠ADB的度数.
如图,△ABC中,BD平分∠ABC,∠ABC=60°,∠C=40°,求∠ADB的度数.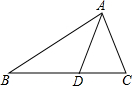 如图,在△ABC中,点D在边BC上,AD=BD=AC,∠BAC=72°,则∠DAC=36°.
如图,在△ABC中,点D在边BC上,AD=BD=AC,∠BAC=72°,则∠DAC=36°.