题目内容
6.当n=1,2,3,4,5,…,2012,2013时,二次函数y=(n2+n)x2-(2n+1)x+1的图象与x轴所截的线段长度之和为( )| A. | $\frac{2011}{2012}$ | B. | $\frac{2012}{2013}$ | C. | $\frac{2013}{2014}$ | D. | $\frac{2014}{2015}$ |
分析 令y=0求得方程的两根分别为x1=$\frac{1}{n}$,x2=$\frac{1}{n+1}$,从而可求得图象与x所截线段的长度为$\frac{1}{n(n+1)}$,然后将n=1,2,3,4,5,…,2012,2013代入,最后求得它们的和即可.
解答 解:令y=0得:(n2+n)x2-(2n+1)x+1=0,
∴(nx-1)[(n+1)x-1]=0.
∴x1=$\frac{1}{n}$,x2=$\frac{1}{n+1}$.
∴图象与x轴所截的线段长度=$\frac{1}{n}-\frac{1}{n+1}$=$\frac{1}{n(n+1)}$.
∴图象与x轴所截的线段长度之和=$\frac{1}{1×2}$+$\frac{1}{2×3}+\frac{1}{3×4}+$…$+\frac{1}{2012×2013}+\frac{1}{2013×2014}$
=1$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$+…$+\frac{1}{2012}-\frac{1}{2013}+\frac{1}{2013}-\frac{1}{2014}$
=1-$\frac{1}{2014}$
=$\frac{2013}{2014}$.
故选:C.
点评 本题主要考查的是二次函数图象与x轴的交点、因式分解法解一元二次方程,利用拆项法求得图象与x轴所截的线段长度之和是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
16.九年级二班50名同学在“爱心捐款”活动中,捐款情况统计如表,
(1)表中a=7;
(2)二班同学捐款数组成的数据中,中位数是12.5、众数是10;
(3)九年级二班50名同学平均捐款多少元?
(4)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
| 捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
| 捐款人数(人) | a | 18 | 10 | 12 | 3 |
(2)二班同学捐款数组成的数据中,中位数是12.5、众数是10;
(3)九年级二班50名同学平均捐款多少元?
(4)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
17.关于抛物线y=x2和y=-x2,下列说法正确的是( )
| A. | 对称轴都是x轴 | B. | 最低点都是原点(0,0) | ||
| C. | 在y轴右侧呈下降趋势 | D. | 形状相同,开口方向相反 |
11.下列说法正确的是( )
| A. | 在Rt△ABC中,∠C=90°,若tanA=$\frac{3}{4}$,则a=3,b=4 | |
| B. | 若△ABC三边之比为1:$\sqrt{3}$:$\sqrt{2}$,且∠A为最小角,则sinA=$\frac{1}{2}$ | |
| C. | 对于锐角α,必有sinα>cosα | |
| D. | 在Rt△ABC中,若∠C=90°,则sin2A+cos2A=1 |
18.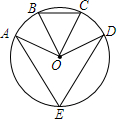 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )| A. | 46° | B. | 68° | C. | 69° | D. | 70° |
16.下列对“0”说法不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 0是最小的整数 | ||
| C. | 0是整数,也是有理 | D. | 0是有理数,也叫中性数 |