题目内容
8.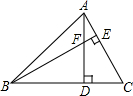 如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
分析 先由已知得到BD=AD,即可证明△BDF≌△ADC,即可求得DF=CD.
解答 解:∵∠ABC=45°,AD⊥BC,
∴BD=AD,
∵∠CAD+∠AFE=90°,∠CAD+∠C=90°,∠AFE=∠BFD,
∴∠AFE=∠C,
在△BDF和△ADC中,
$\left\{\begin{array}{l}{∠CAD=∠FBD}\\{AD=BD}\\{∠BDF=∠ADC}\end{array}\right.$,
∴△BDF≌△ADC(ASA),
∴DF=CD=4.
故选:B.
点评 本题考查了全等三角形的判定、全等三角形对应边相等的性质.解决本题的根据是证明△BDF≌△ADC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.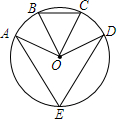 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )| A. | 46° | B. | 68° | C. | 69° | D. | 70° |
19.下列各式是一元二次方程的是( )
| A. | 3-5x2=x | B. | $\frac{3}{x}$+x2-1=0 | C. | ax2+bx+c=0 | D. | 4x-1=0 |
16.下列对“0”说法不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 0是最小的整数 | ||
| C. | 0是整数,也是有理 | D. | 0是有理数,也叫中性数 |
13.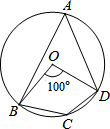 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )| A. | 130° | B. | 100° | C. | 80° | D. | 50° |
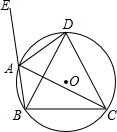 如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.
如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.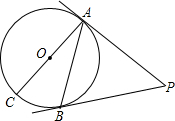 如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,∠BAC=25°.求∠P的度数.
如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,∠BAC=25°.求∠P的度数.