题目内容
7.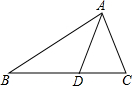 如图,在△ABC中,点D在边BC上,AD=BD=AC,∠BAC=72°,则∠DAC=36°.
如图,在△ABC中,点D在边BC上,AD=BD=AC,∠BAC=72°,则∠DAC=36°.
分析 根据等腰三角形的性质得到∠1=∠B,∠3=∠C,由外角的性质得到∠3=∠1+∠B=2∠B,于是得到∠C=∠3=2∠B,根据三角形的内角和得到∠C=72°,即可得到结论.
解答  解:∵AD=BD=AC,
解:∵AD=BD=AC,
∴∠1=∠B,∠3=∠C,
∵∠3=∠1+∠B=2∠B,
∴∠C=∠3=2∠B,
∵∠BAC=72°,
∴∠B+∠C=180°-72°=108°,
∴∠C=72°,
∴∠DAC=180°-2∠C=36°.
故答案为:36°.
点评 本题考查了等腰三角形的性质,三角形的内角和,三角形外角的性质,熟练则各性质定理是解题的关键.

练习册系列答案
相关题目
17.关于抛物线y=x2和y=-x2,下列说法正确的是( )
| A. | 对称轴都是x轴 | B. | 最低点都是原点(0,0) | ||
| C. | 在y轴右侧呈下降趋势 | D. | 形状相同,开口方向相反 |
18.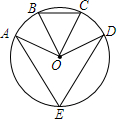 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )| A. | 46° | B. | 68° | C. | 69° | D. | 70° |
19.下列各式是一元二次方程的是( )
| A. | 3-5x2=x | B. | $\frac{3}{x}$+x2-1=0 | C. | ax2+bx+c=0 | D. | 4x-1=0 |
16.下列对“0”说法不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 0是最小的整数 | ||
| C. | 0是整数,也是有理 | D. | 0是有理数,也叫中性数 |
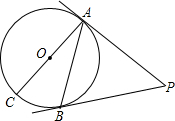 如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,∠BAC=25°.求∠P的度数.
如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,∠BAC=25°.求∠P的度数.