题目内容
10.已知直角三角形的两条直角边长分别为6cm和8cm,则斜边上的高为4.8cm.分析 设斜边上的高为hcm,由勾股定理求出斜边长,再由直角三角形面积的计算方法即可得出斜边上的高.
解答 解:设斜边上的高为hcm,
由勾股定理得:$\sqrt{{6}^{2}+{8}^{2}}$=10cm,
直角三角形的面积=$\frac{1}{2}$×10×h=$\frac{1}{2}$×6×8,
解得:h=4.8.
故答案为:4.8cm.
点评 本题考查了勾股定理、直角三角形面积的计算方法;熟练掌握勾股定理,由直角三角形面积的计算方法得出结果是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.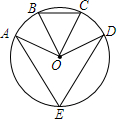 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
 如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )
如图,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED=( )| A. | 46° | B. | 68° | C. | 69° | D. | 70° |
5. 如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:
如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:
①AB=AC=CE;②AB+BD=DE;③AD=$\frac{1}{2}$AE;④BD=DC=CE.
其中,正确的结论是( )
 如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:
如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:①AB=AC=CE;②AB+BD=DE;③AD=$\frac{1}{2}$AE;④BD=DC=CE.
其中,正确的结论是( )
| A. | 只有① | B. | 只有①② | C. | 只有①②③ | D. | 只有①④ |
19.下列各式是一元二次方程的是( )
| A. | 3-5x2=x | B. | $\frac{3}{x}$+x2-1=0 | C. | ax2+bx+c=0 | D. | 4x-1=0 |
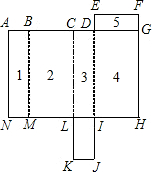 如图所示是长方体的表面展开图,折叠成一个长方体后.
如图所示是长方体的表面展开图,折叠成一个长方体后.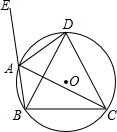 如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.
如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.