题目内容
10.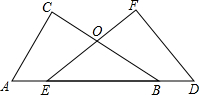 如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD
如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD求证:
(1)BC=EF;
(2)△OEB是等腰三角形.
分析 (1)由垂直的定义证出三角形全等的条件,根据全等三角形的性质得到结论.
(2)根据全等三角形的性质得到对应角相等,再由等腰三角形的判定得到结果.
解答 证明:(1)∵AE=BD,
∴AE+BE=BD+BE,
即:AB=DE,
又∵AC⊥BC,DF⊥EF,
∴∠ACB=∠DFE=90°,
在Rt△ACB和Rt△DFE中,
$\left\{\begin{array}{l}{AC=DF}\\{AB=DE}\end{array}\right.$,
∴Rt△ACB≌Rt△DFE(HL),
∴BC=EF;
(2)由(1)证得Rt△ACB≌Rt△DFE,
∴∠OBE=∠OEB,
∴OE=OB,
∴△OEB是等腰三角形.
点评 本题考查了垂直的定义,全等三角形的判定与性质,等腰三角形判定,证明两直角三角形全等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.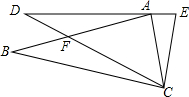 如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
 如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )| A. | DC | B. | BC | C. | AB | D. | AE+AC |
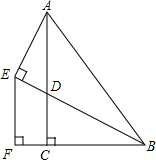 如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,连接BD,过A作AE⊥BD交BD的延长线于E,过E作EF⊥BC交BC的延长线于F,且AC=BF,BE=2AE.
如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,连接BD,过A作AE⊥BD交BD的延长线于E,过E作EF⊥BC交BC的延长线于F,且AC=BF,BE=2AE.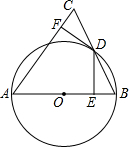 如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.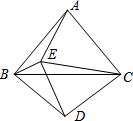 如图.△ABC与△CDE均是等边三角形,若∠DBE=76°,则∠AEB的度数是136°.
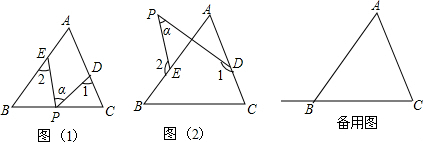
如图.△ABC与△CDE均是等边三角形,若∠DBE=76°,则∠AEB的度数是136°.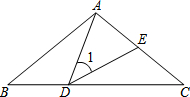 如图,△ABC中,AB=AC=5,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
如图,△ABC中,AB=AC=5,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.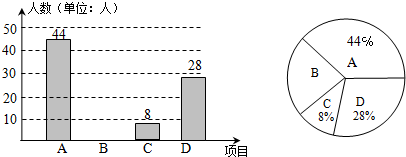
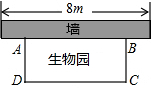 如图,学校打算用材料围建一个面积为18平方米的矩形ABCD的生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米,设AD的长为y米,CD的长为x米.
如图,学校打算用材料围建一个面积为18平方米的矩形ABCD的生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米,设AD的长为y米,CD的长为x米.