题目内容
20.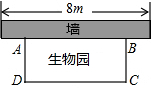 如图,学校打算用材料围建一个面积为18平方米的矩形ABCD的生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米,设AD的长为y米,CD的长为x米.
如图,学校打算用材料围建一个面积为18平方米的矩形ABCD的生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米,设AD的长为y米,CD的长为x米.(1)求y与x之间的函数表达式;
(2)若围成矩形ABCD的生物园的三边材料总长不超过18米,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
分析 (1)根据面积为18m2,可得出y与x之间的函数关系式;
(2)由(1)的关系式,结合x、y都是正整数,可得出x的可能值,再由三边材料总长不超过18m,DC的长<18,可得出x、y的值,继而得出可行的方案.
解答 解:(1)根据题意得xy=18,
即y=$\frac{18}{x}$;
(2)由y=$\frac{18}{x}$,且x、y都是正整数,所以x可取1、2、3、6、9、18,
但x≤8,x+2y≤18,
所以符合条件的有:x=3时,y=6;x=6时,y=3.
答:满足条件的所有围建方案:AD=6m,CD=3m或AD=3m,CD=6m.
点评 本题考查了反比例函数的应用,根据矩形的面积公式得出y与x的函数关系式是关键,第二问注意结合实际解答.

练习册系列答案
相关题目
11.计算:-1-2=( )
| A. | 1 | B. | -1 | C. | -2 | D. | -3 |
5.下列四个多项式,能因式分解的是( )
| A. | a-1 | B. | a2+1 | C. | x2-4y | D. | x2-6x+9 |
10.边长为2的等边三角形的高为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
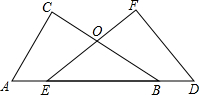 如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD
如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD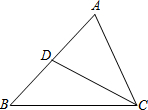 如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求:
如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求: