题目内容
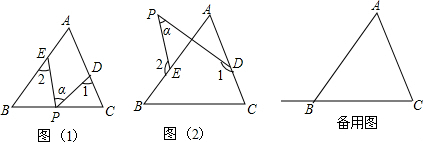
17.在△ABC中,∠A=50°,点D,E分别是边AC,AB上的点(不与A,B,C重合),点P是平面内一动点(P与D,E不在同一直线上),设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在边BC上运动(不与点B和点C重合),如图(1)所示,则∠1+∠2=50°+∠α(用α的代数式表示);
(2)若点P在ABC的外部,如图(2)所示,则∠α,∠1,∠2之间有何关系?写出你的结论,并说明理由.
(3)当点P在边CB的延长线上运动时,试画出相应图形,标注有关字母与数字,并写出对应的∠α,∠1,∠2之间的关系式.(不需要证明)
分析 (1)根据∠AEP=180°-∠2,∠ADP=180°-∠1和四边形AEPD的内角和为360°,表示出∠α,∠1,∠2之间的关系;
(2)根据三角形外角的性质,∠2-∠α=∠1-50°,求出∠α,∠1,∠2之间的关系;
(3)画出符号条件的图形,根据图形和(2)的结论解答即可.
解答 解:(1)∵∠AEP=180°-∠2,∠ADP=180°-∠1,
∴180°-∠2+180°-∠1+∠α+50°=360°,
即∠1+∠2=50°+∠α;
(2)根据三角形外角的性质可知,
∠2-∠α=∠1-50°,
则∠2-∠1=∠α-50°;
(3)如图,
①∠2-∠α=∠1-50°,
则∠2-∠1=∠α-50°;
如图,
②∠1=50°+∠α+∠2,
∠1-∠2=50°+∠α.
点评 本题考查的是三角形内角和定理和三角形的外角的性质的综合运用,灵活运用定理进行计算是解题的关键,在画图时,要全面考虑问题,不要只画出一种.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.2015年1月1日起,杭州市城区实行全新的阶梯水价,之前为了解某社区居民的用水情况,随机对该社区20户居民进行了调查,下表是这20户居民2014年8月份用水量的调查结果:那么关于这次用水量的调查和数据分析,下列说法错误的是( )
| 居民(户) | 1 | 2 | 8 | 6 | 2 | 1 |
| 月用水量(吨) | 4 | 5 | 8 | 12 | 15 | 20 |
| A. | 平均数是10(吨) | B. | 众数是8(吨) | C. | 中位数是10(吨) | D. | 样本容量是20 |
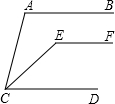 已知:如图AB∥CD,EF∥CD,CE平分∠ACD,∠A=110°,则∠CEF=145°.
已知:如图AB∥CD,EF∥CD,CE平分∠ACD,∠A=110°,则∠CEF=145°.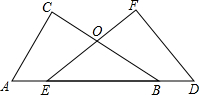 如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD
如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD