Question

1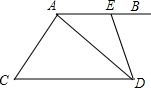．如图，AB∥CD，E为AB上一点，∠BED=2∠BAD．
（1）求证：AD平分∠CDE；
（2）若AC⊥AD，∠ACD+∠AED=165°，求∠ACD的度数．

Answer 1

分析 （1）根据平行线的性质得到∠BED=∠EDC，∠BAD=∠ADC，等量代换得到∠EDC=2∠ADC，由角平分线的定义即可得到结论；
（2）设∠ADC=∠ADE=∠BAD=x，于是得到∠BED=∠EDC=2x，∠AED=180°-2x，根据平行线的性质得到∠BAC+∠ACD=180°，于是列方程90°-x+180°-2X=165°，即可得到结论．

解答 （1）证明：∵AB∥CD，
∴∠BED=∠EDC，∠BAD=∠ADC，
∵∠B E D=∠B A D+∠A D E，
∵∠B ED=2∠B A D，
∴∠B A D=∠A D E，∠A D E=∠A C D，
∴AD平分∠CDE；

（2）解：依题意设∠ADC=∠ADE=∠BAD=x，
∴∠BED=∠EDC=2x，∠AED=180°-2x，
∵AB∥CD，
∴∠BAC+∠ACD=180°，即∠ACD=90°-x，
又∵∠ACD+∠AED=165°，
即90°-x+180°-2X=165°，
∴x=35°，
∴∠ACD=90°-x=90°-35°=55°．

点评 本题考查了平行线的性质，角平分线的判定，熟练掌握平行线的性质是解题的关键．