题目内容
10. 如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.(1)求证:四边形PMEN是平行四边形;
(2)请直接写出当AP为何值时,四边形PMEN是菱形.
分析 (1)由M、N、E分别是PD、PC、CD的中点,根据三角形中位线的性质,可证得ME∥PC,EN∥PD,继而证得四边形PMEN是平行四边形;
(2)由AP=BP=5,可证得△APD≌△BPC(SAS),继而可得PD=PC,则可得PM=EM=EN=PN,继而证得四边形PMEN是菱形.
解答 (1)证明:∵M,E分别为PD,CD的中点,
∴ME∥PC,
同理可证:ME∥PD,
∴四边形PMEN为平行四边形;
(2)解:当PA=5时,四边形PMEN为菱形.
理由:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵AP=5,AB=CD=10,
∴AP=BP,
在△APD和△BPC中,
$\left\{\begin{array}{l}{AP=BP}\\{∠A=∠B}\\{AD=BC}\end{array}\right.$,
∴△APD≌△BPC(SAS),
∴PD=PC,
∵M、N、E分别是PD、PC、CD的中点,
∴EN=PM=$\frac{1}{2}$PD,PN=EM=$\frac{1}{2}$PC,
∴PM=EM=EN=PN,
∴四边形PMEN是菱形.
点评 此题考查了矩形的性质、菱形的判定、全等三角形的判定与性质以及三角形中位线的性质.注意利用三角形中位线的性质求解是关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
18.下列四个命题中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 实数与数轴上的点是一一对应的 | |
| D. | 如果一个数能被2整除,那么它也能被4整除 |
5.已知方程组$\left\{\begin{array}{l}ax-by=4\\ ax+by=2\end{array}\right.$的解为$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$,则3a-2b的值为( )
| A. | 8 | B. | 10 | C. | -10 | D. | -8 |
15.用小数表示3.56×10-7为( )
| A. | 0.000000356 | B. | 0.0000000356 | C. | 0.00000000356 | D. | 0.000000000356 |
19. 如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
 如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )| A. | 60° | B. | 70° | C. | 100° | D. | 120° |

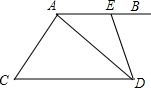 如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.
如图,AB∥CD,E为AB上一点,∠BED=2∠BAD. 小李在参与“设计遮阳篷”的活动中,测得自己家的窗户高AB为1.5米,上网了解到本地区太阳光与地面的最大夹角∠DAE约为73°,最小夹角∠DBF约为28°,请根据所提供的信息,计算出直角形遮阳篷BCD中BC和CD的长度分别为多少米?(结果精确到0.1,参考数据:sin73°≈0.96,cos73°≈0.29,tan73°=≈3.27,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
小李在参与“设计遮阳篷”的活动中,测得自己家的窗户高AB为1.5米,上网了解到本地区太阳光与地面的最大夹角∠DAE约为73°,最小夹角∠DBF约为28°,请根据所提供的信息,计算出直角形遮阳篷BCD中BC和CD的长度分别为多少米?(结果精确到0.1,参考数据:sin73°≈0.96,cos73°≈0.29,tan73°=≈3.27,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)