题目内容
11.已知M=x2+3x-a,N=-x,P=x3+3x2+5,且M•N+P的值与x的取值无关,求a的值.分析 首先根据多项式乘多项式的方法,求出M•N的值是多少;然后用它加上P,求出M•N+P的值是多少;最后根据M•N+P的值与x的取值无关,可得x的系数是0,据此求出a的值是多少即可.
解答 解:M•N+P=(x2+3x-a)•(-x)+(x3+3x2+5)
=-x3-3x2+ax+x3+3x2+5
=ax+5
∵M•N+P的值与x的取值无关,
∴a=0.
点评 此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.如果用平方差公式计算(x-y+5)(x+y+5),则可将原式变形为( )
| A. | [(x-y)+5][(x+y)+5] | B. | [(x-y)+5][(x-y)-5] | C. | [(x+5)-y][(x+5)+y] | D. | [x-(y+5)][x+(y+5)] |
19.计算:$\sqrt{9a}$+$\sqrt{25a}$=( )
| A. | 8$\sqrt{a}$ | B. | $\sqrt{34a}$ | C. | 8a | D. | 15$\sqrt{a}$ |
6.某学校计划用100元钱买乒乓球,所购买球的个数W(个)与单价n(元)的关系式W=$\frac{100}{n}$中( )
| A. | 100是常量,W,n是变量 | B. | 100,W是常量,n是变量 | ||
| C. | 100,n是常量,W是变量 | D. | 无法确定 |
 小明同学起床后,来到院中呼吸一下新鲜空气,突然发现前几天栽好的一颗小树被昨晚的大风刮歪了(如图),小明正想把小树扶正时,突然想起,能否用学过的数学知识求出小树的主根与地面的夹角?能否求出小树被刮歪了多少度?请你帮小明想一想.
小明同学起床后,来到院中呼吸一下新鲜空气,突然发现前几天栽好的一颗小树被昨晚的大风刮歪了(如图),小明正想把小树扶正时,突然想起,能否用学过的数学知识求出小树的主根与地面的夹角?能否求出小树被刮歪了多少度?请你帮小明想一想.
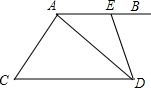 如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.
如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.