题目内容
13.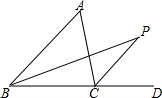 已知在△ABC中,内角∠ABC的平分线与外角∠ACD的平分线交于点P,试说明:∠P=$\frac{1}{2}$∠A.
已知在△ABC中,内角∠ABC的平分线与外角∠ACD的平分线交于点P,试说明:∠P=$\frac{1}{2}$∠A.
分析 利用角平分线定义可知∠PCD=$\frac{1}{2}$∠ACD.再利用外角性质,可得∠ACD=∠A+∠ABC①,∠PCD=∠P+$\frac{1}{2}$∠ABC②,那么可利用∠PCA=∠PCD,可得相等关系.
解答 解:∵CP是∠ACD的角平分线,
∴∠PCD=$\frac{1}{2}$∠ACD.
又∵∠ACD=∠A+∠ABC,
∴∠PCD=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
又∵∠PCD=∠P+$\frac{1}{2}$∠ABC,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=∠P+$\frac{1}{2}$∠ABC,
∴∠P=$\frac{1}{2}$∠A.
点评 本题考查的是三角形内角和定理,利用了角平分线定义、三角形外角性质.三角形的外角等于与它不相邻的两个内角之和等知识.

练习册系列答案
相关题目
4.下列图形中,是轴对称图形但不是中心对称图形的是( )
| A. | 平行四边形 | B. | 圆 | C. | 等腰梯形 | D. | 正方形 |
3.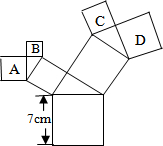 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.
 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.| A. | 3cm2 | B. | 4cm2 | C. | 7cm2 | D. | 49cm2 |
 如图,一段河坝的横截面为梯形ABCD,根据图中数据,可知底宽AD=7.5+4$\sqrt{3}$(单位:m).
如图,一段河坝的横截面为梯形ABCD,根据图中数据,可知底宽AD=7.5+4$\sqrt{3}$(单位:m). 如图,A、B、C三点在数轴上,点C在点A与点B之间,且AC:BC=1:5.
如图,A、B、C三点在数轴上,点C在点A与点B之间,且AC:BC=1:5.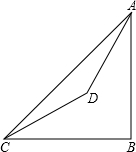 如图,在山脚C测得山顶A的仰角为45°,沿着倾斜角为30°的斜坡前进300米到达D出,D处测得山顶的仰角为60°,求山高AB(结果保留根号).
如图,在山脚C测得山顶A的仰角为45°,沿着倾斜角为30°的斜坡前进300米到达D出,D处测得山顶的仰角为60°,求山高AB(结果保留根号). 如图,AD、BE、CF是⊙O的直径,且∠AOF=∠BOC=∠DOE.弦AB、CD、EF相等吗?为什么?
如图,AD、BE、CF是⊙O的直径,且∠AOF=∠BOC=∠DOE.弦AB、CD、EF相等吗?为什么?